Презентация Исследование функций при помощи производных. Общая схема исследования функции и построения графика онлайн

Содержание слайда: Министерство образования и науки РФ Министерство образования и науки РФ ФГБОУ ВПО «Уральский государственный педагогический университет» Математический факультет Кафедра высшей математики Математика Лекция 8. Исследование функций при помощи производных. Общая схема исследования функции и построения графика Лектор: Бодряков В.Ю. E-mail: Bodryakov_VYu@e1.ru Поток: 1 к. ИКРиМ, 2012-2013 уч.г. Екатеринбург - 2012

Содержание слайда: Рекомендуемая литература Берман Г.Н. Сборник задач по курсу математического анализа: учеб пособие. СПб.: Лань, 2007. – 448 с. Письменный Д.Т. Конспект лекций по высшей математике: [в 2 ч.]. Ч. 1. – М.: Айрис – Пресс, 2008. – 288 с. Тер-Крикоров А.М., Шабунин М.И. Курс математического анализа: учебное пособие для вузов. М.: БИНОМ. Лаборатория знаний, 2009. – 672 с. Фихтенгольц Г.М. Основы математического анализа. Ч. 1. СПб.: Лань, 2005. – 448 с., Ч.2, 2005. – 464 с. Электронный ресурс: www.exponenta.ru

Содержание слайда: Содержание лекции §1. Исследование функций при помощи производных. Возрастание и убывание функции §2. Максимум и минимум функции. Наибольшее и наименьшее значения функции на отрезке §3. Выпуклость графика функции. Точки перегиба §4. Асимптоты графика функции §5. Общая схема исследования функции и построения графика

Содержание слайда: §1. Исследование функций при помощи производных. Возрастание и убывание функции Одним из важных приложений производной является ее применение к исследованию функций. Установим необходимые и достаточные условия возрастания и убывания функции. Т е о р е м а 1 (необходимые условия, ). Если дифференцируемая на интервале (a; b) функция y = f(x) возрастает, то ее первая производная f(x)  0; напротив, если функция f(x) убывает, то ее производная f(x)  0 всюду на интервале (a; b). Доказательство: Пусть функция y = f(x) возрастает на интервале (a; b). Выберем в этом интервале две произвольные точки x и x + x. Рассмотрим отношение = .

Содержание слайда: §1. … Возрастание и убывание функции (продолжение) Функция y = f(x) возрастает, поэтому f(x + x)  f(x) > 0 при x > 0 и, наоборот, f(x + x)  f(x) < 0 при x < 0. В обоих этих случаях = > 0, поэтому и в пределе f(x) = =  0. Аналогично рассматривается случай функции, убывающей на промежутке (a; b), ч.т.д. Геометрически доказанная теорема означает, что касательные к графику возрастающей функции образуют острые углы с положительным направлением оси Ox (см. рис.).

Содержание слайда: §1. … Возрастание и убывание функции (продолжение) Т е о р е м а 2 (достаточные условия, ). Если функция y = f(x) дифференцируема на интервале (a; b) и f(x) > 0, то функция f(x) возрастает; если f(x) < 0, то функция f(x) убывает всюду на интервале (a; b). Доказательство: Пусть f(x) > 0. Возьмем точки x1, x2  (a; b), причем x1 < x2. Применим к отрезку [x1; x2] теорему Лагранжа: f(x2)  f(x1) = f(c)(x2  x1), где c  (x1; x2). По условию теоремы f(c) > 0 и x2  x1 > 0. Следовательно, разность f(x2)  f(x1) > 0 или f(x2) > f(x1) , т.е. функция y = f(x) возрастает на интервале (a; b). Случай f(x) < 0 на интервале (a; b) рассматривается аналогично, ч.т.д. Правило исследования функции y = f(x) на монотонность (монотонное поведение), т.е. на возрастание или убывание. Для того, чтобы исследовать функцию y = f(x) на монотонность необходимо: 1) вычислить производную этой функции y = f(x) и 2) установить интервалы в которых f(x) > 0 и (или) f(x) < 0.

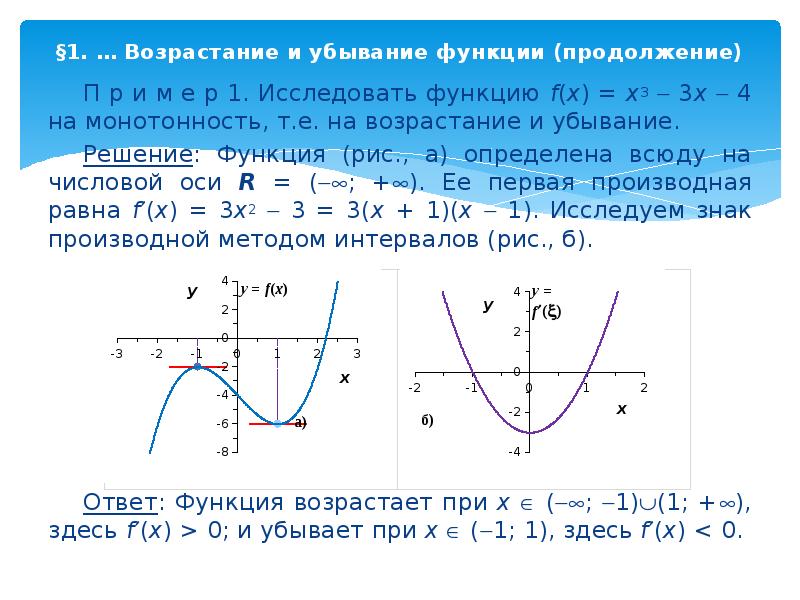
Содержание слайда: §1. … Возрастание и убывание функции (продолжение) П р и м е р 1. Исследовать функцию f(x) = x3  3x  4 на монотонность, т.e. на возрастание и убывание. Решение: Функция (рис., а) определена всюду на числовой оси R = (; +). Ее первая производная равна f(x) = 3x2  3 = 3(x + 1)(x  1). Исследуем знак производной методом интервалов (рис., б). Ответ: Функция возрастает при x  (; 1)(1; +), здесь f(x) > 0; и убывает при x  (1; 1), здесь f(x) < 0.

Содержание слайда: §2. Максимум и минимум функции. Наибольшее и наименьшее значения функции на отрезке Df: Точка x0 называется точкой (локального) максимума функции y = f(x) (см. рис. из примера 1), если существует такая  - окрестность точки x0, то есть интервал (x0  ; x0 + ), что при всех x  x0 из этой окрестности выполняется неравенство f(x) < f(x0). Df: Точка x0 называется точкой (локального) минимума функции y = f(x) (см. рис), если существует такая  - окрестность точки x0, что x  x0 из этой окрестности выполняется неравенство f(x) > f(x0). Df: Значение функции f(x0) в точке x0 максимума (минимума) называется максимумом (минимумом) функции y = f(x). Максимумы и минимумы функции обобщенно называются экстремумами функции.

Содержание слайда: §2. Максимум и минимум функции … (продолжение) Т е о р е м а 3 (П. Ферма, необходимое условие экстремума). Если дифференцируемая функция y = f(x) имеет экстремум в точке x0, то ее производная в этой точке равна нулю: f(x0) = 0. Доказательство: Пусть, для определенности, в точке x0 функция y = f(x) достигает максимума. Тогда в некоторой окрестности точки x0 выполняется неравенство f(x0) > f(x0 + x). Тогда = < 0 при x > 0; и = > 0 при x < 0. По условию теоремы существует производная f(x0) = = , причем в пределе f(x0)  0 при x > 0 и f(x0)  0 при x < 0. Поэтому в самой точке x0 имеем f(x0) = 0, ч.т.д.

Содержание слайда: §2. Максимум и минимум функции … (продолжение) З а м е ч а н и я: 1. Геометрически равенство f(x0) = 0 означает, что в точке x0 экстремума дифференцируемой функции y = f(x) касательная к ее графику параллельна оси Ox (см. рис. к примеру 1). 2. Утверждение, обратное к утверждению теоремы Ферма, в общем случае неверно: из того, что f(x0) = 0 не следует, что в точке x0 функция y = f(x) достигает своего экстремума (экстремальна). Например, для функции y = x3 производная функции равна y = 3x2 = 0 в точке x0 = 0, однако, эта точка не является точкой экстремума (СРС). 3. Существуют функции, которые в точках экстремума не имеют производной. Например, непрерывная функция y = |x| в точке x0 = 0 производной не имеет, но точка x0 – точка минимума (СРС).

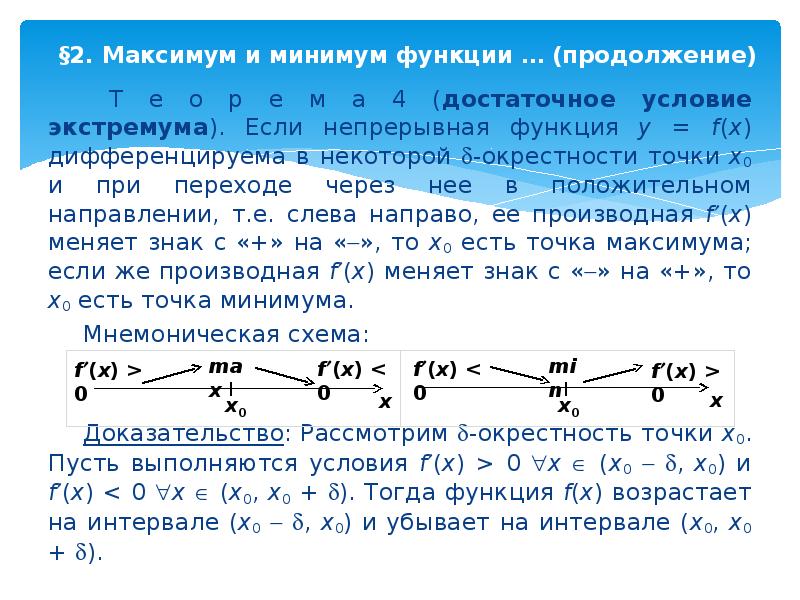
Содержание слайда: §2. Максимум и минимум функции … (продолжение) Т е о р е м а 4 (достаточное условие экстремума). Если непрерывная функция y = f(x) дифференцируема в некоторой -окрестности точки x0 и при переходе через нее в положительном направлении, т.е. слева направо, ее производная f(x) меняет знак с «+» на «», то x0 есть точка максимума; если же производная f(x) меняет знак с «» на «+», то x0 есть точка минимума. Мнемоническая схема: Доказательство: Рассмотрим -окрестность точки x0. Пусть выполняются условия f(x) > 0 x  (x0  , x0) и f(x) < 0 x  (x0, x0 + ). Тогда функция f(x) возрастает на интервале (x0  , x0) и убывает на интервале (x0, x0 + ).

Содержание слайда: §2. Максимум и минимум функции … (продолжение) Отсюда следует, что значение f(x = x0) в точке x0 является наибольшим на интервале (x0  , x0 + ), т.е. f(x) < f(x0) для всех x  (x0  , x0)(x0, x0 + ). Это и означает, что точка x0  точка максимума функции y = f(x). Случай, когда производная функции f(x) меняет в точке x0 знак с «» на «+», рассматривается аналогично, ч.т.д. Правила исследования функции на экстремум: 1) Найти критические точки функции y = f(x). 2) Выбрать из них лишь те, которые являются внутренними точками области определения функции D. 3) Исследовать знак производной f(x) слева и справа от каждой из выбранных критических точек. 4) В соответствии с теоремой о достаточном условии экстремума выписать точки экстремума, если они есть, и вычислить значения функции в каждой из них.

Содержание слайда: §2. Максимум и минимум функции … (продолжение) П р и м е р 2. Найти экстремумы функции y =  . Решение: Областью определения функции является все множество действительных чисел D = R. Находим y = (  ) =   = . Производная не существует при x1 = 0 и равна 0 при x2 = 8. Эти точки разбивают область определения функции на три интервала: (; 0), (0; 8), (8; +). Отметим на рис. знаки производной, полученные, например, методом пробных точек, слева и справа от критических точек x1 и x2: Ответ: В т. x1 = 0 – max f(0) = 0; в т. x2 = 8 – min f(8) = 4/3.

Содержание слайда: §2. Максимум и минимум функции … (продолжение) Иногда бывает удобным использовать другой достаточный признак существования экстремума функции y = f(x), основанный на анализе знака второй производной f(x). Т е о р е м а 5. Если в точке x0 первая производная дважды дифференцируемой функции y = f(x) равна нулю (f(x0) = 0), а 2-ая производная отлична от нуля (f(x0)  0), то при f(x0) < 0 в точке x0 функция имеет максимум, а при f(x0) > 0 – минимум. Мнемоническая схема:

Содержание слайда: §2. Максимум и минимум функции … (продолжение) Доказательство: Пусть для определенности f(x0) > 0. Поскольку f(x0) = = > 0, то > 0 в достаточно малой окрестности точки x0. Если x < 0, то f(x0 + x) < 0; если x > 0, то f(x0 + x) > 0. Таким образом, при переходе через точку x0 первая производная f(x) меняет знак с минуса на плюс. Значит, по теореме 4, в точке x0 функция y = f(x) достигает своего минимума. Аналогично доказывается, что если f(x0) < 0, то в точке x0 функция y = f(x) имеет максимум, ч.т.д.

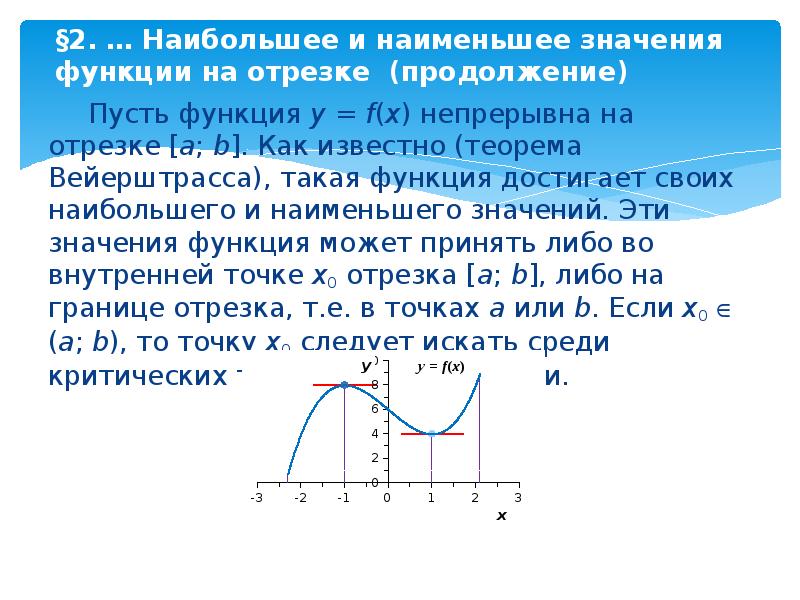
Содержание слайда: §2. … Наибольшее и наименьшее значения функции на отрезке (продолжение) Пусть функция y = f(x) непрерывна на отрезке [a; b]. Как известно (теорема Вейерштрасса), такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке x0 отрезка [a; b], либо на границе отрезка, т.е. в точках a или b. Если x0  (a; b), то точку x0 следует искать среди критических точек данной функции.

Содержание слайда: §2. … Наибольшее и наименьшее значения функции на отрезке (продолжение) Правила исследования функции y = f(x), заданной на отрезке [a; b] на наибольшее и наименьшее значения: 1) Найти критические точки функции y = f(x) на интервале (a; b). 2) Вычислить значения функции в найденных критических точках. 3) Вычислить значения функции на концах отрезка, т.е. в точках x = a и x = b. 4) Среди всех вычисленных значений функции выбрать наибольшее и наименьшее. З а м е ч а н и е. Если функция не имеет критических точек на промежутке (a; b), то такая функция монотонно возрастает или убывает, достигая своих наибольшего и наименьшего значений на концах отрезка [a; b].

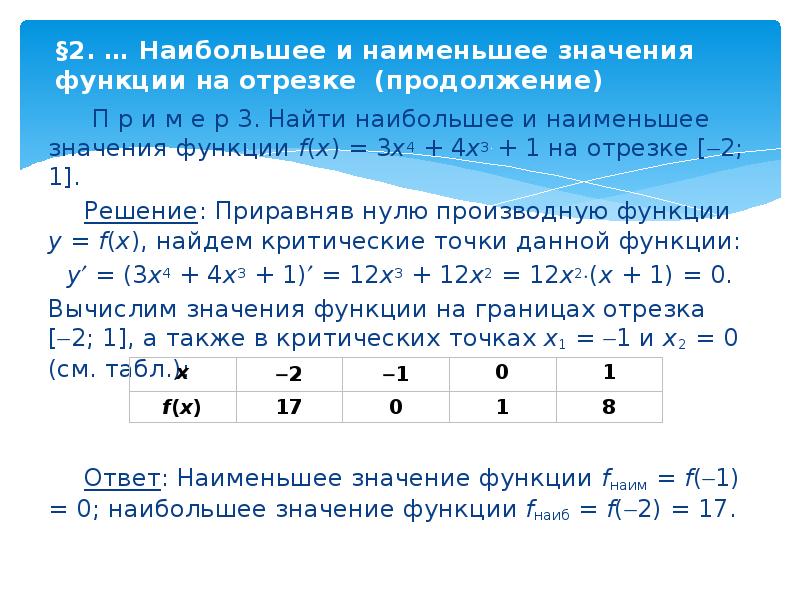
Содержание слайда: §2. … Наибольшее и наименьшее значения функции на отрезке (продолжение) П р и м е р 3. Найти наибольшее и наименьшее значения функции f(x) = 3x4 + 4x3 + 1 на отрезке [2; 1]. Решение: Приравняв нулю производную функции y = f(x), найдем критические точки данной функции: y = (3x4 + 4x3 + 1) = 12x3 + 12x2 = 12x2(x + 1) = 0. Вычислим значения функции на границах отрезка [2; 1], а также в критических точках x1 = 1 и x2 = 0 (см. табл.): Ответ: Наименьшее значение функции fнаим = f(1) = 0; наибольшее значение функции fнаиб = f(2) = 17.

Содержание слайда: §2. … Наибольшее и наименьшее значения функции на отрезке (продолжение) П р и м е р 4. Из шара объемом V0 необходимо выточить цилиндр наибольшего объема V. Чему он равен? Решение: Объем шара равен V0 = R3, так что его радиус равен R = . Установим размеры вписанного в шар цилиндра наибольшего объема, т.е. диаметр x его основания и высоту y (см. рис.). Объем вписанного цилиндра равен V = x2y, а размеры x и y цилиндра связаны с радиусом R теоремой Пифагора: x2 + y2 = 4R2.

Содержание слайда: §2. … Наибольшее и наименьшее значения функции на отрезке (продолжение) Исключая переменную x, получим выражение для целевой функции – объема цилиндра V  в виде функции одной переменной: V = (4R2  y2)y, где 0  y  2R. Найдем максимум данной функции по переменной y: V = (4R2  3y2) = 0 при y2 = R2 или y = R. Соответствующее значение диаметра x дается выражением: x2 = 4R2  y2 = 4R2  R2 = R2. Объем цилиндра равен: V = x2y =  R2R = R3 = V0. Вторая производная V =  y < 0 – отрицательна при y > 0, т.е. найден именно максимум целевой функции. Ответ: Вписанный в шар наибольший цилиндр имеет объем, равный V = V0.

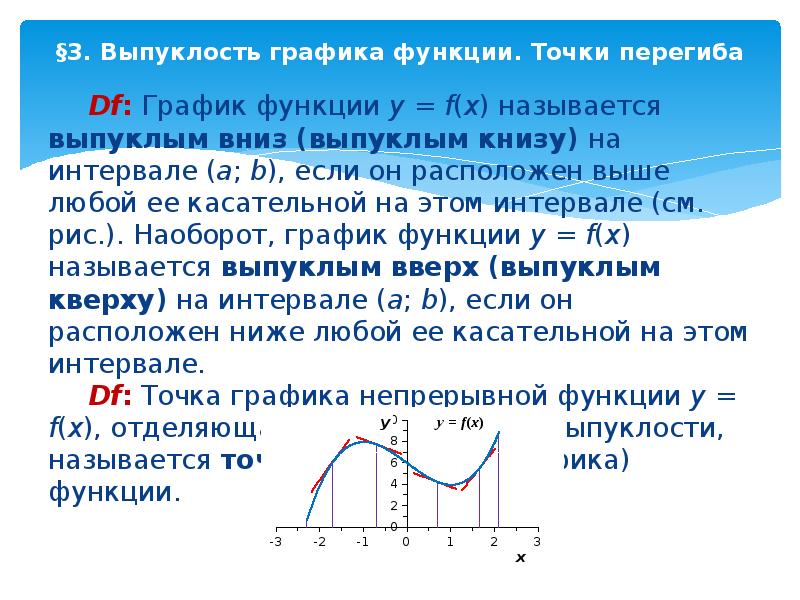
Содержание слайда: §3. Выпуклость графика функции. Точки перегиба Df: График функции y = f(x) называется выпуклым вниз (выпуклым книзу) на интервале (a; b), если он расположен выше любой ее касательной на этом интервале (см. рис.). Наоборот, график функции y = f(x) называется выпуклым вверх (выпуклым кверху) на интервале (a; b), если он расположен ниже любой ее касательной на этом интервале. Df: Точка графика непрерывной функции y = f(x), отделяющая его части разной выпуклости, называется точкой перегиба (графика) функции.

Содержание слайда: §3. Выпуклость графика функции. Точки перегиба Интервалы выпуклости вниз и вверх находят с помощью следующей теоремы. Т е о р е м а 6. Если дважды дифференцируемая функция y = f(x) во всех точках интервала (a; b) имеет отрицательную вторую производную, т.е. f(x0) < 0, то график функции в этом интервале выпуклый вверх. Если же f(x0) > 0 x  (a; b) – график выпуклый вниз. Доказательство: СРС.

Содержание слайда: §3. Выпуклость графика функции. Точки перегиба (продолжение) Для нахождения точек перегиба графика функции используется следующая теорема. Т е о р е м а 7 (достаточное условие существования точек перегиба). Если у дважды дифференцируемой функции y = f(x) 2-ая производная f(x0) при переходе через точку x0, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой x0 есть точка перегиба. Доказательство: Пусть f(x) < 0 при x < x0 и f(x) > 0 при x > x0. Это значит, что слева от точки x = x0 график выпуклый вверх, а справа – выпуклый вниз. Следовательно, точка (x0; f(x0)) графика является точкой перегиба, ч.т.д. Аналогично доказывается, что если f(x) > 0 при x < x0 и f(x) < 0 при x > x0, то точка (x0; f(x0))  точка перегиба.

Содержание слайда: §3. Выпуклость графика функции. Точки перегиба (продолжение) П р и м е р 7. Исследовать на выпуклость и точки перегиба график функции y = x3  3x + 6. Решение: Найдем первую и вторую производные функции и приравняем последнюю нулю: y = (x3  3x + 6) = 3x2  3 = 3(x2  1). y = 6x = 0 при x0 = 0. Ясно, что y < 0 при x < 0, здесь график функции y(x) выпуклый вверх, и y > 0 при x > 0, здесь график функции y(x) выпуклый вниз. Точка x0 = 0 – точка перегиба. Ответ: Точка x0 = 0 – точка перегиба (см. график на первом слайде §3).

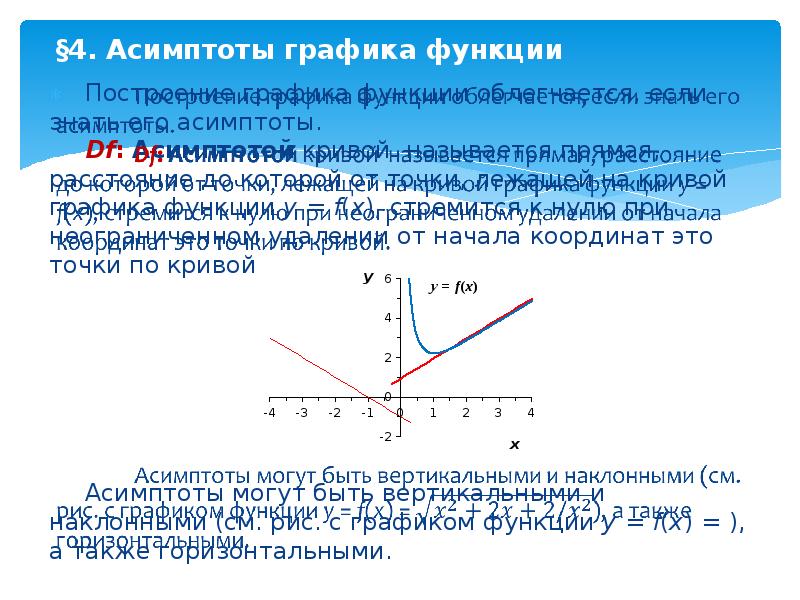
Содержание слайда: §4. Асимптоты графика функции Построение графика функции облегчается, если знать его асимптоты. Df: Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой графика функции y = f(x), стремится к нулю при неограниченном удалении от начала координат это точки по кривой. Асимптоты могут быть вертикальными и наклонными (см. рис. с графиком функции y = f(x) = ), а также горизонтальными.

Содержание слайда: §4. Асимптоты графика функции (продолжение) Df: Говорят, что прямая x = a является вертикальной асимптотой графика функции y = f(x), если = , или = , или = . Правило отыскания вертикальных асимптот: Для отыскания вертикальных асимптот графика функции y = f(x) следует найти те значения x, вблизи которых функция f(x) по модулю неограниченно возрастает. Обычно такие точки являются точками разрывов второго рода. Так, кривая функции y = имеет вертикальную асимптоту x = 1, ибо =  и = +.

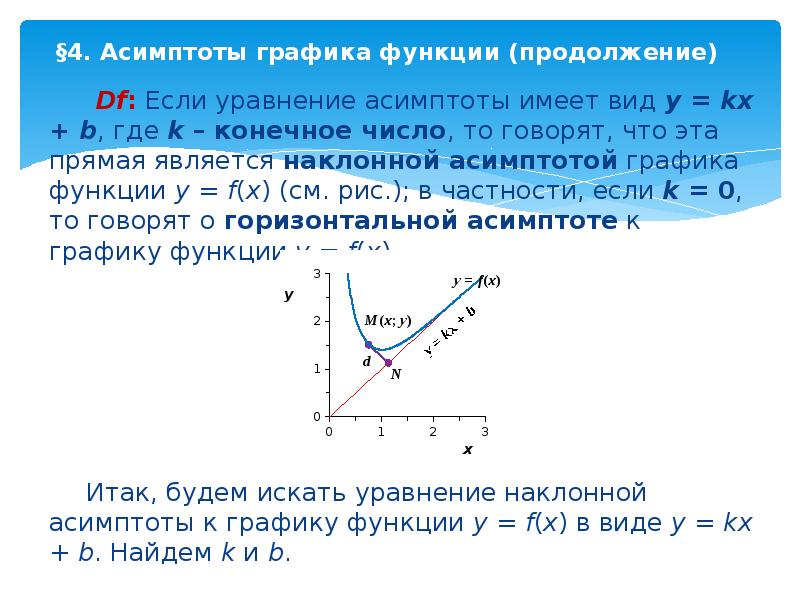
Содержание слайда: §4. Асимптоты графика функции (продолжение) Df: Если уравнение асимптоты имеет вид y = kx + b, где k – конечное число, то говорят, что эта прямая является наклонной асимптотой графика функции y = f(x) (см. рис.); в частности, если k = 0, то говорят о горизонтальной асимптоте к графику функции y = f(x). Итак, будем искать уравнение наклонной асимптоты к графику функции y = f(x) в виде y = kx + b. Найдем k и b.

Содержание слайда: §4. Асимптоты графика функции (продолжение) Пусть M(x; y) – произвольная точка кривой y = f(x). Из аналитической геометрии на плоскости известно, что расстояние от точки M(x; y) до прямой y = kx + b дается выражением: d = . Для наклонной асимптоты параметр k является конечным числом, поэтому условие d  0 при x   выполняется, если к нулю стремится числитель дроби: = 0. Отсюда следует, что разность под знаком модуля может быть представлена в виде kx  y + b = , где  = (x) – б.м.ф., т.е.   0 при x  . Разделив обе части равенства kx  y + b =  на x и переходя к пределу при x  , получим: = = k.

Содержание слайда: §4. Асимптоты графика функции (продолжение) Выразив угловой коэффициент асимптоты k: k = , получим затем выражение для свободного члена b: b = . Правило отыскания наклонных асимптот: Для отыскания наклонных асимптот y = kx + b графика функции y = f(x) необходимо последовательно вычислить коэффициенты асимптоты по формулам: k = , b = . З а м е ч а н и е: Асимптоты функции y(x) при x   и x   могут быть, вообще говоря, различными. Поэтому необходимо рассматривать оба случая x  .

Содержание слайда: §4. Асимптоты графика функции (продолжение) П р и м е р 8. Найти асимптоты функции y = x(ex  1). Решение: Действуя по указанному выше правилу отыскания наклонных асимптот, найдем k и b: k+ = = = = , k = = = = -1 + = -1. Т.о., при x   асимптоты нет, а при x   угловой коэффициент k = 1. Для этого случая найдем свободный член: b = = = = 0. У графика функции y = x(ex  1) при x   имеется наклонная асимптота y = x. Ответ: У графика функции y = x(ex  1) при x   имеется наклонная асимптота y = x; при x  + асимптоты нет.

Содержание слайда: §5. Общая схема исследования функции и построения графика Исследование функции y = f(x) целесообразно вести в определенной последовательности (см. далее). З а м е ч а н и я: 1. Приведенная схема исследования является общей и, в зависимости от конкретного вида исследуемой функции, в простых случаях некоторые пункты могут быть опущены. 2. Если построение графика функции остается затруднительным даже проведения полного исследования функции, следует вычислить и построить дополнительно несколько точек графика, выявить другие особенности поведения функции. 3. Иногда целесообразно исследование функции сопровождать постепенным построением эскиза графика функции y = f(x).

Содержание слайда: §5. Общая схема исследования функции … (продолжение) Правила (схема) исследования функции y = f(x) и построения ее графика: 1) Найти область определения функции. 2) Найти точки пересечения графика с осями координат. 3) Найти интервалы знакопостоянства функции, т.е. интервалы, на которых f(x) > 0 и f(x) < 0. 4) Установить четность и (или) периодичность функции. 5) Найти асимптоты графика функции. 6) Найти интервалы монотонности функции. 7) Найти экстремумы функции. 8) Найти интервалы выпуклости и точки перегиба функции. 9) На основании проведенного исследования построить график функции y = f(x).

Содержание слайда: §5. Общая схема исследования функции … (продолжение) П р и м е р 9. Построить график функции y = . Решение: Выполним все пункты схемы. 1. Функция не определена при x1 = 1 и при x2 = 1. Область определения функции D = (; 1)(1; 1)(1; +); график состоит из 3-х ветвей. 2. Если x = 0, то y = 0, т.е. график функции y(x) пересекает координатные оси в точке O(0; 0). 3. Установим интервалы знакопостоянства функции. Функция y(x) знакоположительна при условиях: y(x) = > 0  (I)  (II) . Решение неравенства y(x) > 0 есть объединение двух решений: решения системы (I) (0; +)(1; 1) = (0; 1) и решения системы (II): (; 0)((; 1)(1; +)) = (; 0). Т.о., y(x) > 0 при x  (; 0)(0; 1). Аналогично, y(x) < 0 при x  (1; 0)(1; +).

Содержание слайда: §5. Общая схема исследования функции … (продолжение) 4. Функция y = является нечетной, так как y(x) = =  = y(x). Следовательно, график функции y(x) симметричен относительно оси Ox. 5. Прямые x = 1 и x = 1 являются вертикальными асимптотами функции. Действительно, = +; = ; = +; = . Выясним наличие наклонных асимптот: k = = = 0, b = = = 0. Т.о., у графика y(x) есть горизонтальная асимптота y = 0.

Содержание слайда: §5. Общая схема исследования функции … (продолжение) 6. Находим интервалы возрастания и убывания функции по знаку первой производной: y = () = = . Очевидно, y = > 0 x  D, т.е. функция y(x) всюду возрастает. 7. Исследуем функцию y(x) на наличие экстремумов. В силу п.6 y > 0 x  D, т.е. локальных экстремумов у функции нет. Производная данной функции y(x) не существует в точках x1 = 1 и x2 = 1, однако эти точки не входят в область D определения функции. 8. Исследуем функцию на выпуклость. Найдем y: y = () = = .

Содержание слайда: §5. Общая схема исследования функции … (продолжение) Вторая производная y(x) равна нулю или не существует в точках x1 = 1, x2 = 1, x3 = 0. В последней точке y(x3 = 0) = 0. Исследуем знак второй производной методом интервалов, решая неравенства: y = > 0 и y = < 0. Получим: y(x) > 0 при x  (; 1)(0; 1) – здесь функция выпукла вниз; y(x) < 0 при x  (1; 0)(1; +) – здесь y(x) выпукла вверх. 9. На основании исследования строим график функции y(x) = (см. рис.).

Содержание слайда: Спасибо за внимание! Ваши вопросы, замечания, предложения …