Презентация Статистическая термодинамика онлайн
На нашем сайте вы можете скачать и просмотреть онлайн доклад-презентацию на тему Статистическая термодинамика абсолютно бесплатно. Урок-презентация на эту тему содержит всего 56 слайдов. Все материалы созданы в программе PowerPoint и имеют формат ppt или же pptx. Материалы и темы для презентаций взяты из открытых источников и загружены их авторами, за качество и достоверность информации в них администрация сайта не отвечает, все права принадлежат их создателям. Если вы нашли то, что искали, отблагодарите авторов - поделитесь ссылкой в социальных сетях, а наш сайт добавьте в закладки.
Презентации » Образование » Статистическая термодинамика
Оцените!
Оцените презентацию от 1 до 5 баллов!
- Тип файла:ppt / pptx (powerpoint)
- Всего слайдов:56 слайдов
- Для класса:1,2,3,4,5,6,7,8,9,10,11
- Размер файла:586.00 kB
- Просмотров:71
- Скачиваний:2
- Автор:неизвестен
Слайды и текст к этой презентации:
№2 слайд


Содержание слайда: Занятие №1. Некоторые предварительные сведения
Система СИ
В основном при расчетах следует придерживаться системы единиц СИ.
Основные единицы СИ:
Физ.вел-на назв.ед. обозн. символ
Длина метр м l
Масса килограмм кг m
Время секунда с t
Кол-во в-ва моль моль n
Терм-ская т-ра кельвин К T
№4 слайд


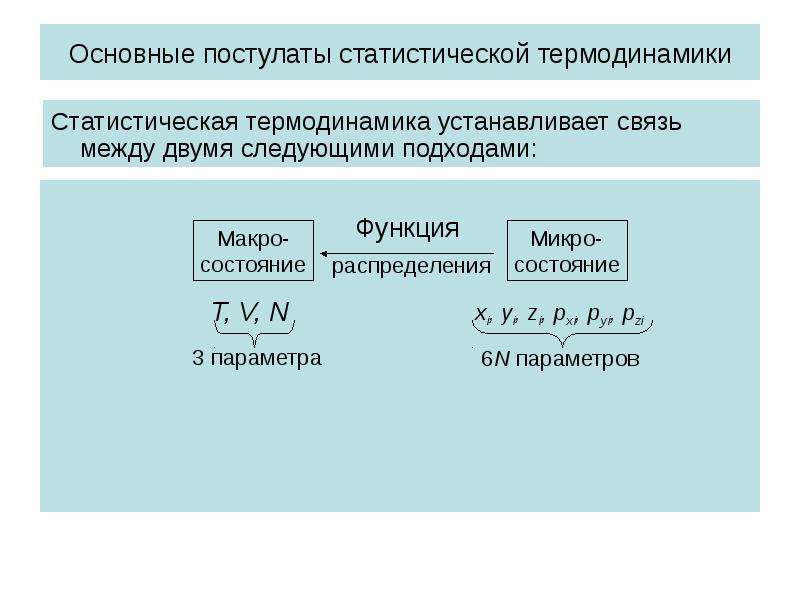
Содержание слайда: Статистическая термодинамика
Замечание (продолжение)
Количество вещества не является синонимом массы.
Количество вещества и масса – две независимые
физические величины, являющиеся основными
физическими величинами СИ.
Любое вещество состоит из формульных (структурных) единиц или частиц (аббревиатура ФЕ).
№5 слайд


Содержание слайда: Статистическая термодинамика
Замечание (продолжение)
Формульные единицы в химии – это реально существующие частицы, такие как атомы, молекулы, ионы, радикалы, условные молекулы кристаллических веществ (KCl).
Количество вещества B (символ nB или n(B), единица моль) – физическая величина, пропорциональная числу формульных единиц этого вещества (NФЕ):
nB = NФЕ/NA ,
где NA – постоянная Авогадро.
№6 слайд


Содержание слайда: Статистическая термодинамика
Замечание (продолжение)
Один моль – это такое количество вещества, которое содержит столько ФЕ, сколько атомов содержится в
0.012 кг изотопа углерода .Число атомов в 12 г углерода
равно постоянной Авогадро, NA= 6.022045 ·1023 моль-1.
Кстати, слово «моль» после числа и в заголовках таблиц не склоняется. Например, 6 моль, 0.12 моль, а не 6 молей, 0.12 молей. Называть физическую величину nB «числом молей» неправильно, поскольку nB представляет собой обозначение величины, а не число. Не следует в термине «количество вещества» опускать слово «вещество» или переставлять слова. Правильно: «количество вещества 1 моль».
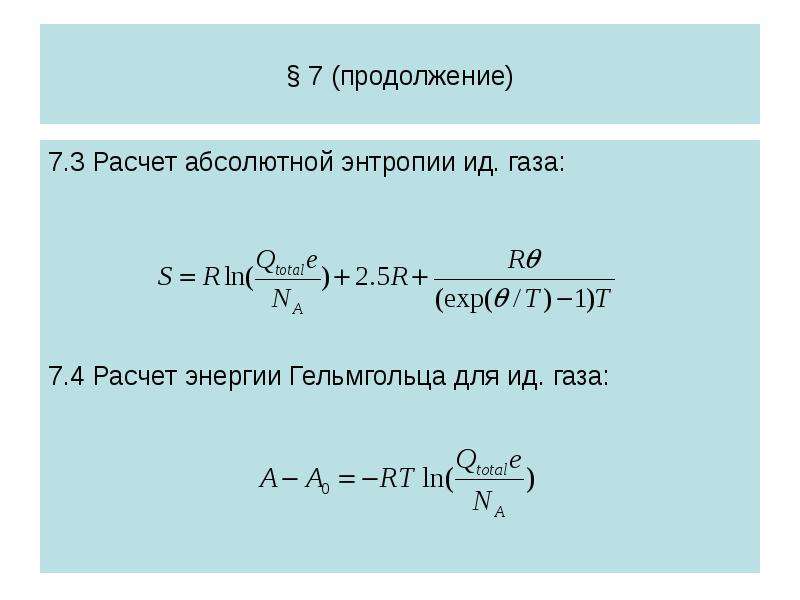
№7 слайд


Содержание слайда: Статистическая термодинамика
Замечание (продолжение)
Масса атома (символ na ,единица – а.е.м.) – масса, измеряемая в относительных единицах, - атомных единицах массы; 1 а.е.м. = 1/12 массы атома изотопа углерода ,масса которого точно равна 12 а.е.м. В а.е.м. измеряют массы молекул. атомных ядер и элементарных частиц:
1 а.е.м. = 1.66057 ·10 -27 кг .
Ввиду малости а.е.м. удобным макроскопическим числом атомов является число NA атомов массой 1 а.е.м., которые вместе имеют массу 1 грамм :
NA = 1/(1 а.е.м) = (1г)/(1.66057·10-24 г) = 6.022045 · 1023
№8 слайд


Содержание слайда: Статистическая термодинамика
2. Необходимые элементы комбинаторики
Перестановки- это соединения элементов, отличающиеся порядком их расположения.
Число различных перестановок N элементов равно
PN = N!
Размещения – это соединения, отличающиеся как самими элементами, так и их порядком.
Число различных размещений из N элементов по n равно
№9 слайд


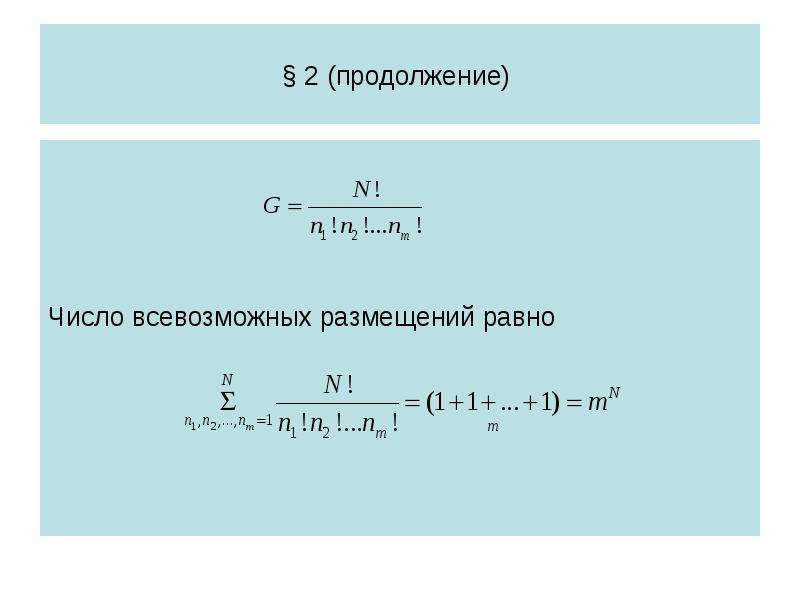
Содержание слайда: § 2 (продолжение)
Сочетания – это соединения, отличающиеся только элементами, но не их порядком.
Число различных сочетаний из N элементов по n равно
Размещение по ячейкам. Пусть имеется N различных элементов, которые нужно разместить по m различным ячейкам. Если в i-ю ячейку (i = 1,2,3,…,m) попадает точно ni элементов, причем n1+n2+…+nm = N, то число таких размещений равно
№14 слайд


Содержание слайда: Необходимые сведения из химической термодинамики
1. Законы термодинамики.
1-ый закон термодинамики:
dU = δQ-δA, U – внутренняя энергия, Q и A – функции перехода – теплота и работа, соответственно. Выбор знаков- Q положительна, если она передается системе; A положительна, если она совершается системой над окружающей средой.
2-ой закон термодинамики: Существует функция состояния – энтропия S, которая обладает свойством
,
где знак равно относится к обратимым процессам, а знак больше – к необратимым.
№15 слайд


Содержание слайда: Продолжение предыдущего слайда
3-ий закон термодинамики (постулат Планка):
При абсолютном нуле (T=0 K) все идеальные кристаллы имеют одинаковую энтропию, равную нулю.
2. Термодинамические потенциалы.
Термодинамическими потенциалами (характкристическими функциями) называют термодинамические функции, с помощью которых и их производных по соответствующим независимым переменным (естественным) могут быть выражены в явном виде все термодинамические свойства системы.
№16 слайд


Содержание слайда: Продолжение предыдущего слайда
Четыре основных термодинамических потенциала:
Внутренняя энергия U(S,V)
ЭнтальпияH(S,p)=U+pV
Энергия Гельмгольца F(T,V)=U-TS
Энергия Гиббса G(T,p)=H-TS=F+pV,
В скобках указаны естественные переменные. Зависимость указанных потенциалов от естественных переменных описывается основным уравнением термодинамики, которое объединяет первый и второй законы термодинамики.
Если ограничиться закрытыми системами, в которых не происходят химические реакции и совершается только механическая работа, основное уравнение можно записать в четырех эквивалентных формах:
№17 слайд


Содержание слайда: Продолжение предыдущего слайда
dU=TdS-pdV (1), dH=TdS+Vdp (2), dF=-pdV-SdT (3),
dG=Vdp-SdT (4).
Если система открыта или в системе происходят химические реакции, то надо учесть зависимость термодинамических потенциалов от количества вещества ni . Например, если G=f(T,p,n1,n2,…), то
dG=-SdT+Vdp+Σμi dni (5), где
№25 слайд


Содержание слайда: Примеры
Молекула может находиться на двух уровнях с энергиями 0 и 300 см-1. Какова вероятность того, что молекула будет находиться на верхнем уровне при 250 о С?
2. В некоторой молекуле есть три электронных уровня: 0, 1500 и 2800 см-1 . Нижний уровень невырожден, средний – трехкратно вырожден, высший – пятикратно вырожден. Найдите среднюю электронную энергию молекулы (см-1 ) и заселенность нижнего уровня при температуре 1900 К. Значение постоянной hc/k = 1,44 см К.
№26 слайд


Содержание слайда: Расчет сумм по состояниям и термодинамических функций двухатомных молекул квантово-статистическим методом
§1. Основные понятия. Формулы.
Исходное понятие статистического метода – термодинамическая вероятность W . Это число различных равновероятных микросостояний системы, соответствующих данному макросостоянию.
Для системы из N неразличимых частиц
№27 слайд


Содержание слайда: §1 (продолжение)
Где Ni – число молекул с энергией εi , gi – статистический вес i – го энергетического уровня, S – абсолютная энтропия, k – константа Больцмана.
На основе вышеприведенных формул для изолированной равновесной системы, состоящей из N слабо взаимодействующих молекул, может быть получено выражение закона распределения молекул по энергиям Максвелла-Больцмана (см. слайд №24), который лежит в основе статистического метода вычисления термодинамических функций. В этом законе распределения знаменатель представляет собой т.н. молекулярную сумму по состояниям:
№28 слайд


Содержание слайда: §1(продолжение)
Q – безразмерная величина, численное значение которой зависит от температуры, объема системы, от массы, размеров и характера движения молекул. Молекула, состоящая более чем из одного атома, одновременно совершает различные движения: поступательное (как целое), вращательное, колебательное, движение системы электронов.
Полная (внутренняя) энергия молекулы (моля) идеального газа величина аддитивная. Таким образом, для i – й молекулы:
εi (total) ≡ Ui = εt,i + [εr + εv +εel ]i = εt,i + εi (in)
Для N молекул:
№29 слайд


Содержание слайда: §1 (продолжение)
Сумма по состояниям – величина мультипликативная, поэтому
Q(total)=Qt [Qr Qv Qel ]=Qt Q(in)
или
lnQ(total)=lnQt + lnQr + lnQv + lnQel
В силу своей мультипликативности сумма по состояниям системы, состоящей из N различных молекул, связана с суммой по состояниям одной молекулы выражением
ZN = QN (ZN называют большой суммой по состояниям)
Для системы из N неразличимых частиц в выражение для ZN следует ввести поправку N!≈(N/e)N :
ZN = (QN)/N!=(Qe/N)N
№30 слайд


Содержание слайда: §1 (продолжение)
Примечание. Множитель e/N обычно включают в поступательную сумму по состояниям, т.к. она присуща молекулам всех типов.
Тогда для lnZN получаем:
lnZN = N ln(Q(total)e/N) = N(ln(Qte/N)+lnQ(in))
Примечание. При вычислении термодинамических функций, которые связаны с lnZN , сомножитель N обычно берется равным числу Авогадро NA .
№31 слайд


Содержание слайда: §2. Расчет молекулярной суммы по состояниям для поступательного движения
В квантовой механике показывается, что для поступательного движения частицы в одномерном потенциальном ящике ее энергия связана с массой частицы и шириной потенциального ящика уравнением:
εt,x = (n2 h2)/(8ml2),
где n – квантовое число, принимающее значения от 1 до ∞, h – постоянная Планка, m – масса частицы, l – ширина потенциального ящика.
Сумма по состояниям поступательного движения вдоль оси x Qt,x должна быть подсчитана по всем возможным значениям квантового числа n :
№34 слайд


Содержание слайда: §2 (продолжение)
Для трехмерного потенциального ящика, имеющего форму куба, последнее уравнение можно преобразовать к виду:
Qt,xyz =Qt,x Qt,y Qt,z = [(2πmkT)3/2 l3]/h3=[(2πmkT)3/2V]/h3 ,
где V – объем ящика.
Полученное уравнение справедливо не только для контейнера кубической формы, но и для любой другой. Если учесть уравнение состояния идеального газа, то для одного моля получим:
Qt = [(2πmkT)3/2RT]/(h3p)
При умеренных температурах Qt очень большое число.
№35 слайд


Содержание слайда: §2 (продолжение)
Замечание. Возможность перехода от суммирования к интегрированию обусловлена тем, что величина
h2/ (8mV2/3) в случае макроскопического объема очень мала. Так, при V = 1 см3 она составляет ≈ 6·10-34 Дж для электрона, ≈ 10-37Дж для атома гелия и еще меньше для более тяжелых атомов.
Поскольку kT = 1.38·10-23T Дж, то уже при T=1 K и для более высоких температур
h2/(8mV2/3kT)«1, так что поступательный спектр можно считать квазинепрерывным и пользоваться квазинепрерывным приближением. Замена единицы на ноль для нижнего предела интегрирования практически не сказывается на величине интеграла, но облегчает его вычисление.
№37 слайд


Содержание слайда: §3. Расчет молекулярной суммы по состояниям для вращательного движения
В качестве модели двухатомной молекулы можно выбрать два атома А и В с массами mA и mB, находящихся на фиксированном расстоянии r0 друг от друга. Такая система называется жестким ротатором. Если подобная система вращается вокруг оси, проходящей через центр тяжести О перпендикулярно к линии, соединяющей ядра, то выражение для момента инерции имеет вид.
I0=mA(r0-x)2 +mBx2 ,
где x – расстояние от атома В до центра тяжести молекулы. Если записать выражение для моментов относительно О, то mA(r0-x)=mBx . Отсюда
x=(mAr0)/(mA+mB)
№38 слайд


Содержание слайда: §3 (продолжение)
Следовательно,
I0=mA(r0-(mAr0)/(mA+mB))2+mB(mAr0/(mA+mB))2=
(mAmB/(mA+mB))ro2
Приведенная масса молекулы выражается как
(1/) = (1/mA)+(1/mB). Отсюда = mAmB/(mA+mB).
Тогда выражение для момента инерции принимает вид
I0 = r02. (3.1)
Это означает, что двухатомную молекулу, вращающуюся вокруг своего центра тяжести, можно рассматривать как одну частицу с массой , описывающую круг радиуса r0 .
Движение частицы по кругу – задача, для которой можно найти точное решение уравнения Шредингера.
№39 слайд


Содержание слайда: § 3 (продолжение)
Это решение дает следующее выражение для вращательной энергии
r = J(J+1)h2/8π2I0 = J(J+1)hBe (3.2) , где Be= h/8π2I0 .
Величина Be называется вращательной постоянной.
Вращательное квантовое число J может принимать целочисленные значения, включающие нуль (0,1,…∞).
Степень вырождения каждого уровня равна gr=2J+1 и представляет собой число различных ориентаций механического момента вращения молекулы относительно выделенного направления – межъядерного расстояния.
С помощью формулы (3.2) выражение для вращательной суммы по состояниям принимает вид.
№41 слайд


Содержание слайда: § 3 (продолжение)
Интегрирование дает следующее выражение
Qr= (8π2IkT)/h2 (3.4)
Формула (3.4) выведена для гетероядерных молекул. Для гомоядерных молекул при повороте на каждые 180 0 мы будем иметь две неразличимые конфигурации. Вследствие этого уравнение (3.4) увеличивает число состояний в два раза. Чтобы учесть это (3.4) преобразуют к виду
Qr= (8π2IkT)/ σh2 , (3.5)
где σ – число симметрии. Оно равно числу неразличимых состояний при повороте молекулы вокруг оси симметрии на 360 0 (для гомоядерных оно равно 2, а для гетероядерных – 1)
№42 слайд


Содержание слайда: § 4. Расчет молекулярной суммы по состояниям для колебательного движения
Колебательное движение двухатомной молекулы будем рассматривать в рамках модели гармонического осциллятора. Для этого случая можно точно решить уравнение Шредингера и получить колебательные уровни энергии в виде:
v = (v+1/2)h0 , (4.1)
где 0 – собственная (основная) частота колебания,
v – колебательное квантовое число, может принимать целочисленные значения, включая нуль. Уровни энергии равно отстоят друг от друга и при v=0
v,0 = h0/2. Эта величина и является нулевой энергией колебательного движения.
№43 слайд


Содержание слайда: § 4 (продолжение)
Классическая частота колебания гармонического осциллятора связана с приведенной массой (двухатомная молекула) и силовой постоянной k0 уравнением:
0 = ( 1/2π)√k0/ (4.2)
Поскольку колебательное движение в случае двухатомной молекулы не вырождено (gv = 1), то сумма по состояниям дается выражением:
№45 слайд


Содержание слайда: § 4 (продолжение)
Если ввести характеристическую колебательную температуру θ = h0/k , то можно записать
qv =1/(1-exp(-θ/T) (4.4)
Часто пользуются не частотой, а волновым числом ωe , которое равно ωe = 1/ = /c , где c – скорость света.
Тогда
qv = 1/(1-exp(-hcωe /kT) (4.5)
№48 слайд


Содержание слайда: § 5.Расчет молекулярной суммы по состояниям для электронного движения
В общем случае выражение для молекулярной суммы по состояниям для электронного движения имеет вид
где hνi – энергия возбуждения, ε0 –энергия основного электронного состояния, принимаемая равной нулю, g0 –степень вырождения или статистический вес основного энергетического состояния (терма), gi и εi – соответственно, статистические веса и энергии возбужденных электронных состояний. Из опыта известно, что в случае двух и многоатомных молекул
№49 слайд


Содержание слайда: § 5 (продолжение)
вклад возбужденных состояний в величину статистической суммы при умеренных температурах (< 2000 К) в большинстве случаев является пренебрежимо малым. Таким образом, можно допустить
Qel = g0 (5.1).
Статистический вес основного состояния двухатомной молекулы находят из данных о величине суммарного орбитального момента количества движения электронов (L) и мультиплетности терма основного электронного состояния.
Электронные состояния молекул классифицируют по значениям квантового числа (Λ).
№50 слайд


Содержание слайда: § 5 (продолжение)
При заданной величине L оно может принимать значения Λ = 0,1,2,…,L. Состояния, отвечающие значениям квантового числа Λ, равным 0,1,2, обозначаются, соответственно, как Σ-, Π- и Δ-состояния.
Кроме величины Λ, электронные состояния молекулы характеризуются, как и у атомов, значениями мультиплетности электронного состояния (2S+1), котороая связана с числом неспаренных электронов. Мультиплетность электронного состояния указывается в виде верхнего индекса слева от буквенного обозначения состояния:
№51 слайд


Содержание слайда: § 5 (продолжение)
Статистический вес для термов вида Σ находят из выражения g0 = 2S+1, для термов Π и Δ – из выражения g0 = 2(2S+1).
Состояния 1Σ с компенсированными спинами (2·0 + 1)=1 называются синглетными, состояния 2Σ, 2Π, 2Δ – дублетными и 3Σ, 3Π, 3Δ – триплетными.
Пример. Для молекулы HCl терм основного состояния
1Σ, следовательно для нее g0=1, для O2 терм 3Σ и g0=3,
для TiO терм 3Δ и g0=6.
Скачать все slide презентации Статистическая термодинамика одним архивом:
Похожие презентации
-
 Термодинамика и статистическая физика
Термодинамика и статистическая физика -
 Колебания. Молекулярная физика. Статистическая термодинамика.
Колебания. Молекулярная физика. Статистическая термодинамика. -
 Наглядное представление статистической информации
Наглядное представление статистической информации -
 Использование статистических методов при изучении отношения школьников к математике. Автор работы: ученица 9Г класса СОШ 2 горо
Использование статистических методов при изучении отношения школьников к математике. Автор работы: ученица 9Г класса СОШ 2 горо -
 Совещание территориальных органов Росстата по вопросам разработки итогов выборочного федерального статистического наблюдения
Совещание территориальных органов Росстата по вопросам разработки итогов выборочного федерального статистического наблюдения -
 На тему "Статистический анализ качества знаний школьников" - скачать презентации по Педагогике
На тему "Статистический анализ качества знаний школьников" - скачать презентации по Педагогике -
 На тему "Статистическое исследование стиля обучения и мышления" - скачать презентации по Педагогике
На тему "Статистическое исследование стиля обучения и мышления" - скачать презентации по Педагогике -
 Кафедра «Бухгалтерский учет и аудит» Ослопова М. В. ТЕМА 9. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ДИНАМИКИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ
Кафедра «Бухгалтерский учет и аудит» Ослопова М. В. ТЕМА 9. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ДИНАМИКИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ -
 Кафедра «Бухгалтерский учет и аудит» Ослопова М. В. ТЕМА 8. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИ
Кафедра «Бухгалтерский учет и аудит» Ослопова М. В. ТЕМА 8. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВЗАИМОСВЯЗИ СОЦИАЛЬНО-ЭКОНОМИЧЕСКИХ ЯВЛЕНИ -
 ТЕМА 7. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВАРИАЦИИ
ТЕМА 7. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ВАРИАЦИИ