Презентация Понятие и принципы построения математической модели физических систем онлайн
На нашем сайте вы можете скачать и просмотреть онлайн доклад-презентацию на тему Понятие и принципы построения математической модели физических систем абсолютно бесплатно. Урок-презентация на эту тему содержит всего 23 слайда. Все материалы созданы в программе PowerPoint и имеют формат ppt или же pptx. Материалы и темы для презентаций взяты из открытых источников и загружены их авторами, за качество и достоверность информации в них администрация сайта не отвечает, все права принадлежат их создателям. Если вы нашли то, что искали, отблагодарите авторов - поделитесь ссылкой в социальных сетях, а наш сайт добавьте в закладки.
Презентации » Физика » Понятие и принципы построения математической модели физических систем
Оцените!
Оцените презентацию от 1 до 5 баллов!
- Тип файла:ppt / pptx (powerpoint)
- Всего слайдов:23 слайда
- Для класса:1,2,3,4,5,6,7,8,9,10,11
- Размер файла:184.05 kB
- Просмотров:104
- Скачиваний:1
- Автор:неизвестен
Слайды и текст к этой презентации:
№3 слайд


Содержание слайда: В первую очередь нам необходимо сформулировать физическую модель. Колебание маятника не равномерное: в какой-то момент времени груз движется быстро, а в другой момент времени медленнее. Такое ускоренное движение, согласно второму закону Ньютона, может происходить только под действием внешней силы, в противном случае груз совершал бы, согласно принципу Галилея, прямолинейное равномерное движение. Попытаемся выяснить, какие силы здесь задействованы. Груз электрически нейтрален, значит, на него не могут действовать электрические и магнитные поля. Из гравитационных полей существенный вклад вносится только со стороны Земли. Солнце и остальные планеты, как легко показать, действуют на маятник со значительно меньшими силами, и ими с высокой точностью можно пренебречь.
№4 слайд


Содержание слайда: Есть еще силы трения, в первую очередь, сила трения о воздух. При малых скоростях движения груза эта сила пропорциональна скорости и плотности воздуха. Коэффициент пропорциональности очень мал. Сила трения существенно меньше силы притяжения Земли и ею можно пренебречь, только если рассматриваются колебания в относительно небольшие времена. Это обусловлено специфическим характером сил трения, под действием которых из системы непрерывно уходит энергия. За большой промежуток времени маятник может потерять значительную часть своей энергии и это потеря скажется на движении маятника как заметное падение амплитуды колебания.
К малозначительным факторам, влияющим на движение маятника, отнесем и вращение Земли. Тогда можно считать маятник совершающим движение в одной плоскости, образованной осями Оx и Оy декартовой системы координат.
№5 слайд


Содержание слайда: Если за Fx и Fy обозначить проекции вектора силы притяжения Земли на оси координат x и y, то согласно механике Ньютона уравнения движения маятника будут иметь вид
где m – масса маятника.
Но мы воспользуемся механикой Лагранжа, так как нахождение всех компонентов сил в более сложной системе относительно трудоемкая работа.
Для нашего маятника
№6 слайд


Содержание слайда: где g – ускорение свободного падения; l – длина нити. Отсчет потенциальной энергии ведется от нижнего положения равновесия. Символами x и y здесь обозначены координаты груза. Так как груз совершает движение по дуге окружности, заданной уравнением x2 + y2 = l2, то функции x(t) и y(t) во-первых, не являются независимыми переменными, во-вторых, удобно перейти в полярную систему координат по формулам
где g – ускорение свободного падения; l – длина нити. Отсчет потенциальной энергии ведется от нижнего положения равновесия. Символами x и y здесь обозначены координаты груза. Так как груз совершает движение по дуге окружности, заданной уравнением x2 + y2 = l2, то функции x(t) и y(t) во-первых, не являются независимыми переменными, во-вторых, удобно перейти в полярную систему координат по формулам
№8 слайд


Содержание слайда: Определим функцию Лагранжа:
Функция Лагранжа зависит от двух переменных , d/dt. При выводе уравнения Эйлера – Лагранжа в общем случае под x мы подразумевали координату, но не уточняли, что понимается под словом координата и о какой системе (декартовой, полярной и т.д.) идет речь. Для уравнения Эйлера – Лагранжа это не принципиально. Применительно к колебанию маятника мы это уравнение можем записать в виде
№9 слайд


Содержание слайда: Вычисление здесь соответствующих производных приводит к уравнению колебания математического маятника:
которое должно быть дополнено начальными условиями для угла и его скорости.
Колебания, описываемые уравнением не затухают со временем, так как мы не учитывали явление трения.
№10 слайд


Содержание слайда: Если тело при взаимодействии с другими телами (или средами) увеличивает их кинетическую энергию, то тело испытывает силу сопротивления, если же уменьшает, то на тело будет действовать ускоряющая сила.
Если тело при взаимодействии с другими телами (или средами) увеличивает их кинетическую энергию, то тело испытывает силу сопротивления, если же уменьшает, то на тело будет действовать ускоряющая сила.
Т.к. качающийся маятник приводит в движение воздух, что легко обнаружить, то мы сразу же заключаем, что маятник испытывает силу сопротивления, которое иначе называют еще силой трения.
В науке о движении жидкостей – гидродинамике доказано, что сила Fc сопротивления, действующая со стороны среды на тело, зависит от его геометрических форм, относительной скорости V тела и среды, ее плотности и физической характеристики, называемой вязкостью .
№11 слайд


Содержание слайда: Характер силы гидродинамического сопротивления определяется одним безразмерным параметром Re, который называется числом Рейнольдса. Для тела достаточно малого размера L и скорости V если Re = LV/ << 1, то сила Fc прямо пропорциональна V: Fc ~ V. Пусть груз маятника имеет форму шара с радиусом а. С точностью до числового множителя порядка единицы силу сопротивления можно вычислить по формуле
Характер силы гидродинамического сопротивления определяется одним безразмерным параметром Re, который называется числом Рейнольдса. Для тела достаточно малого размера L и скорости V если Re = LV/ << 1, то сила Fc прямо пропорциональна V: Fc ~ V. Пусть груз маятника имеет форму шара с радиусом а. С точностью до числового множителя порядка единицы силу сопротивления можно вычислить по формуле
Fc = a V.
№12 слайд


Содержание слайда: Так как идет речь о простейшей модели маятника, то мы вместо V подставим окружную скорость самого маятника, а влияние скорости воздуха на величину силы сопротивления и других параметров будем считать учтенным в коэффициенте пропорциональности k = a. Тогда в полярных координатах имеем
№13 слайд


Содержание слайда: где отрицательный знак означает, что сила Fc тормозящая. С учетом этой силы трения уравнение движения маятника будет выглядеть следующим образом:
где отрицательный знак означает, что сила Fc тормозящая. С учетом этой силы трения уравнение движения маятника будет выглядеть следующим образом:
= k/m.
Рассмотренный пример с математическим маятником не демонстрирует всех достоинств механики Лагранжа. Уравнение (1) можно легко получить и в рамках механики Ньютона. Приведем другой пример маятника с подвижной точкой подвеса, где подход Лагранжа существенно упрощает вывод уравнений движения, по сравнению с подходом Ньютона. На рисунке 3 точка подвеса маятника с массой m1 без трения скользит по горизонтальной поверхности. Массу подвешенного груза обозначим за m2.
№14 слайд


Содержание слайда: Координату тела массы m1 обозначим за y, а координаты груза m2 – за x2 и y2. По рисунку 3 определяем
Координату тела массы m1 обозначим за y, а координаты груза m2 – за x2 и y2. По рисунку 3 определяем
Учитывая, что величины x2, y2 и зависят от времени, определим производные:
№15 слайд


Содержание слайда: являющиеся компонентами скорости подвешенного груза. Скорость движения подвеса равна dy/dt. Тогда полная кинетическая энергия системы T равна сумме кинетической энергии движения грузов с массами m1 и m2:
являющиеся компонентами скорости подвешенного груза. Скорость движения подвеса равна dy/dt. Тогда полная кинетическая энергия системы T равна сумме кинетической энергии движения грузов с массами m1 и m2:
№16 слайд


Содержание слайда: Вклад в полную потенциальную энергию U дает только подвешенный груз:
Вклад в полную потенциальную энергию U дает только подвешенный груз:
Искомые уравнения движения из функции Лагранжа
где неизвестными параметрами механической системы являются угол и смещение y подвеса, получаются из дифференциальных соотношений
№18 слайд


Содержание слайда: В приведенной форме эти уравнения не удобны для численного решения. Чтобы привести их в нормальную форму необходимо из первого уравнения с помощью второго исключить d2/dt2. Аналогичным образом поступаем и со вторым уравнением. Простой расчет дает
В приведенной форме эти уравнения не удобны для численного решения. Чтобы привести их в нормальную форму необходимо из первого уравнения с помощью второго исключить d2/dt2. Аналогичным образом поступаем и со вторым уравнением. Простой расчет дает
m = m1 +m2.
№19 слайд


Содержание слайда: #include<conio.h>
#include<stdio.h>
#include<math.h>
float omeg= 3;
float Fx(float x, float v, float t);
float Fv(float x, float v, float t);
int main()
{
FILE *f;
f=fopen ("D:\\Inf\\dif_2.dat", "w");
float x0, x, xp, xt, xn, h, t, tc;
float v0, v, vp, vn;
x0=0; v0=5.25;
tc=10.0;
h=0.01;
№20 слайд


Содержание слайда: x=x0; v=v0; //nach uslovie
x=x0; v=v0; //nach uslovie
for (t=0; t<tc; t=t+h)
{
xt=v0/omeg*sin(omeg*t);
printf (" t= %.3f, x= %.3f xt= %.3f \n", t, x, xt);
fprintf (f,"%.3f %.3f %.3f\n", t, x, xt);
xn=x; vn=v;
xp= xn +h*Fx(xn,vn, t);
vp= vn +h*Fv(xn,vn, t);
x= xn +0.5*h*(Fx(xn, vn, t)+Fx(xp, vp, t+h));
v= vn +0.5*h*(Fv(xn, vn, t)+Fv(xp, vp, t+h));
}
getch();
}
Скачать все slide презентации Понятие и принципы построения математической модели физических систем одним архивом:
Похожие презентации
-
 Построение и исследование физических моделей в Delphi 7
Построение и исследование физических моделей в Delphi 7 -
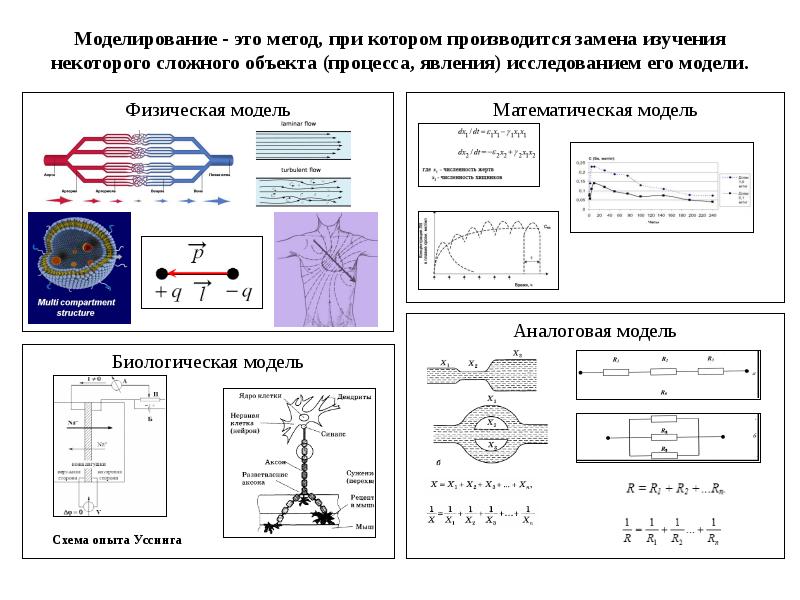 Физическая, математическая, аналоговая, биологическая модели процессов. Моделирование. (Лекция 1)
Физическая, математическая, аналоговая, биологическая модели процессов. Моделирование. (Лекция 1) -
 Лабораторные работы по курсу «Математическое моделирование технических систем»
Лабораторные работы по курсу «Математическое моделирование технических систем» -
 Принципы построения систем и организации радиосвязи
Принципы построения систем и организации радиосвязи -
 Голография Её физические принципы
Голография Её физические принципы -
 Принцип действия тепловых двигателей. КПД тепловых двигателей Цель урока: раскрыть физические принципы действия тепловых двигат
Принцип действия тепловых двигателей. КПД тепловых двигателей Цель урока: раскрыть физические принципы действия тепловых двигат -
 Информационно-исследовательский проект по физике «Основные физические величины системы СИ» Авторы: учащиеся 7 «Г» класса :Бахт
Информационно-исследовательский проект по физике «Основные физические величины системы СИ» Авторы: учащиеся 7 «Г» класса :Бахт -
 Введение в физику с неньютоновым временем На основе холистского системного принципа единства синтеза и анализа рассмотрено обоб
Введение в физику с неньютоновым временем На основе холистского системного принципа единства синтеза и анализа рассмотрено обоб -
 Эксперимент и моделирование – основные физические методы исследовАния природы
Эксперимент и моделирование – основные физические методы исследовАния природы -
 Физические величины. Международная система единиц. Измерительные приборы. Глава 1. Физические методы исследования природы
Физические величины. Международная система единиц. Измерительные приборы. Глава 1. Физические методы исследования природы






