Презентация Параллелограммы: ромб, прямоугольник, квадрат онлайн

На нашем сайте вы можете скачать и просмотреть онлайн доклад-презентацию на тему Параллелограммы: ромб, прямоугольник, квадрат абсолютно бесплатно. Урок-презентация на эту тему содержит всего 12 слайдов. Все материалы созданы в программе PowerPoint и имеют формат ppt или же pptx. Материалы и темы для презентаций взяты из открытых источников и загружены их авторами, за качество и достоверность информации в них администрация сайта не отвечает, все права принадлежат их создателям. Если вы нашли то, что искали, отблагодарите авторов - поделитесь ссылкой в социальных сетях, а наш сайт добавьте в закладки.

Презентации » Математика » Параллелограммы: ромб, прямоугольник, квадрат

Просмотр ВСЕЙ презентации! ЖМИТЕ

Оцените презентацию от 1 до 5 баллов!

Смотреть онлайн
Скачать

Тип файла:

ppt / pptx (powerpoint)
Всего слайдов:

12 слайдов
Для класса:

1,2,3,4,5,6,7,8,9,10,11
Размер файла:

217.38 kB
Просмотров:

84
Скачиваний:

1
Автор:

неизвестен

Слайды и текст к этой презентации:

№1 слайд

Содержание слайда: Параллелограммы

№2 слайд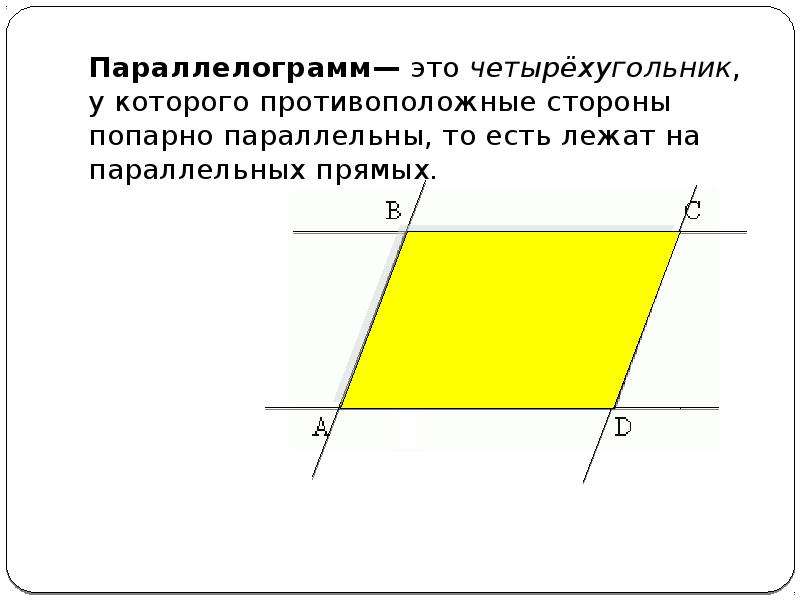

Содержание слайда: Параллелограмм— это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.

№3 слайд

Содержание слайда: Противоположные стороны параллелограмма равны. Противоположные углы параллелограмма равны. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.. Сумма углов, прилежащих к одной стороне, равна 180°. Точка пересечения диагоналей является центром симметрии параллелограмма. Биссектриса отсекает от параллелограмма равнобедренный треугольник. Сумма всех углов равна 360°. Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.

№4 слайд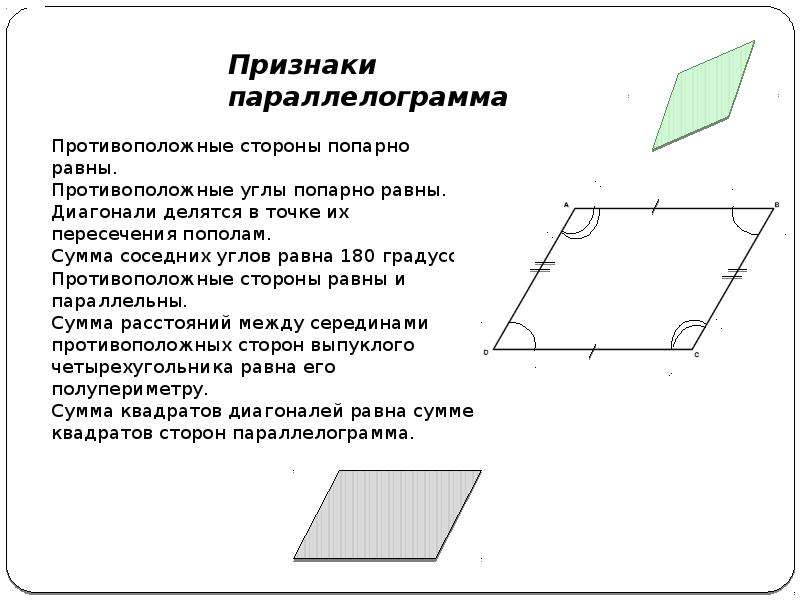

Содержание слайда: Противоположные стороны попарно равны. Противоположные углы попарно равны. Диагонали делятся в точке их пересечения пополам. Сумма соседних углов равна 180 градусов. Противоположные стороны равны и параллельны. Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полупериметру. Сумма квадратов диагоналей равна сумме квадратов сторон параллелограмма.

№5 слайд

Содержание слайда: Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам). Примечание. В евклидовой геометрии для того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые. Четвёртый угол (в силу теоремы о сумме углов многоугольника) также будет равен 90°. В неевклидовой геометрии, где сумма углов четырёхугольника не равна 360° — прямоугольников не существует.

№6 слайд

Содержание слайда: Прямоугольник является параллелограммом — его противоположные стороны попарно параллельны. Стороны прямоугольника являются его высотами. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (по теореме Пифагора). Около любого прямоугольника можно описать окружность, причем диагональ прямоугольника равна диаметру описанной окружности (радиус равен полудиагонали).

№7 слайд

Содержание слайда: Параллелограмм является прямоугольником, если выполняется любое из условий: Если диагонали параллелограмма равны. Если квадрат диагонали параллелограмма равен сумме квадратов смежных сторон. Если углы параллелограмма равны.

№8 слайд

Содержание слайда: Ромб — это параллелограмм, у которого все стороны равны. Ромб с прямыми углами называется квадратом.

№9 слайд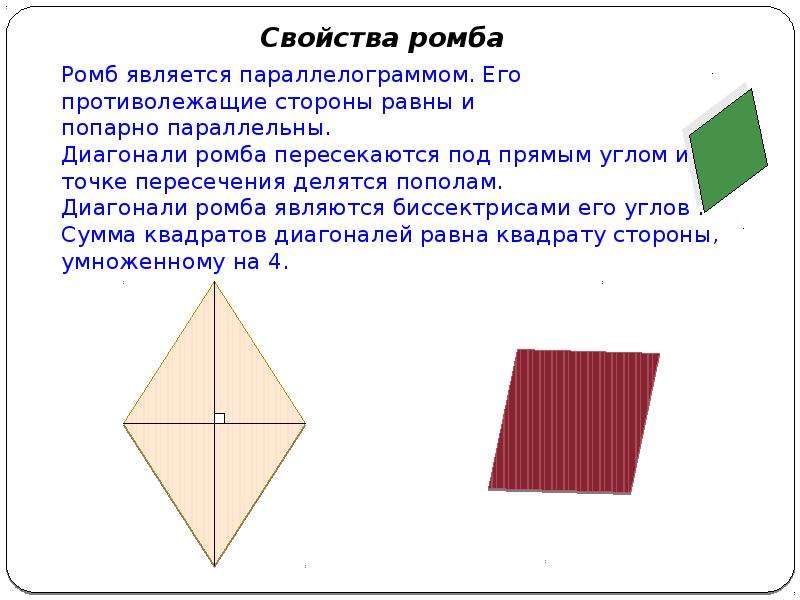

Содержание слайда: Ромб является параллелограммом. Его противолежащие стороны равны и попарно параллельны. Диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам. Диагонали ромба являются биссектрисами его углов . Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4.

№10 слайд

Содержание слайда: Параллелограмм является ромбом, если выполняется одно из следующих условий: Все его стороны равны. Его диагонали пересекаются под прямым углом . Его диагональ делит его угол пополам.

№11 слайд