Презентация Высшая математика. Учебно-методическое пособие для подготовки к компьютерному тестированию. 2 семестр онлайн
На нашем сайте вы можете скачать и просмотреть онлайн доклад-презентацию на тему Высшая математика. Учебно-методическое пособие для подготовки к компьютерному тестированию. 2 семестр абсолютно бесплатно. Урок-презентация на эту тему содержит всего 93 слайда. Все материалы созданы в программе PowerPoint и имеют формат ppt или же pptx. Материалы и темы для презентаций взяты из открытых источников и загружены их авторами, за качество и достоверность информации в них администрация сайта не отвечает, все права принадлежат их создателям. Если вы нашли то, что искали, отблагодарите авторов - поделитесь ссылкой в социальных сетях, а наш сайт добавьте в закладки.
Оцените презентацию от 1 до 5 баллов!
- Тип файла:ppt / pptx (powerpoint)
- Всего слайдов:93 слайда
- Для класса:1,2,3,4,5,6,7,8,9,10,11
- Размер файла:1.74 MB
- Просмотров:77
- Скачиваний:0
- Автор:неизвестен
Слайды и текст к этой презентации:
№1 слайд
Содержание слайда: §5. Системы линейных уравнений
№2 слайд
Содержание слайда: 6.1. Основные понятия
Системой линейных алгебраических уравнений, содержащей m уравнений и n неизвестных называется система вида
№3 слайд
Содержание слайда: Систему (1) удобно записывать в компактной матричной форме:
Систему (1) удобно записывать в компактной матричной форме:
Где - матрица
коэффициентов
системы
№4 слайд
Содержание слайда: - вектор-столбец неизвестных.
- вектор-столбец неизвестных.
№5 слайд
Содержание слайда: ОПР. Расширенной матрицей системы (1) называется матрица системы, дополненная столбцом свободных членов
ОПР. Расширенной матрицей системы (1) называется матрица системы, дополненная столбцом свободных членов
№6 слайд
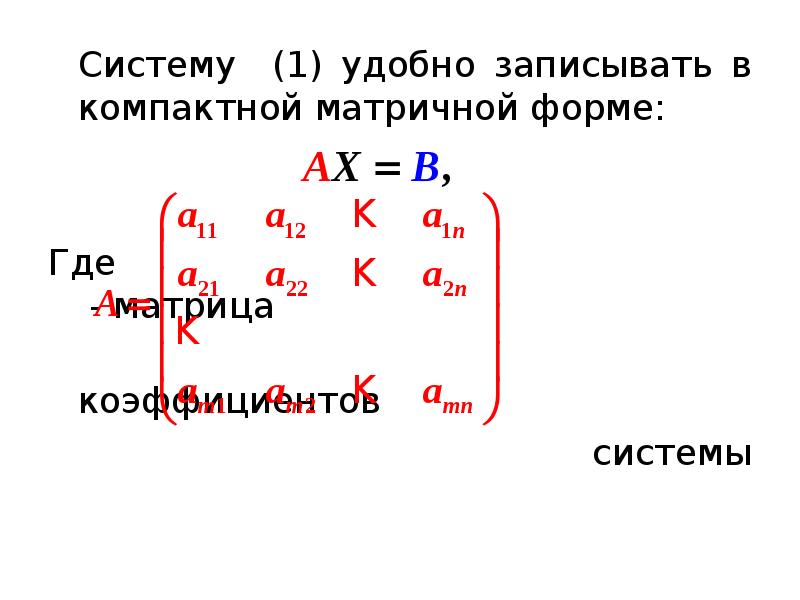
Содержание слайда: Решение системы
Упорядоченное множество чисел
называется решением системы (1), если каждое из уравнений системы обращается в верное равенство после подстановки вместо соответственно чисел
Система уравнений называется совместной, если она имеет хотя бы одно решение. Система, не имеющая ни одного решения, называется несовместной.
№7 слайд
Содержание слайда: Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
В последнем случае каждое ее решение называется частным решением системы.
Совокупность всех частных решений называется общим решением.
№8 слайд
Содержание слайда: Решить систему – это значит выяснить совместна она или несовместна. Если система совместна, найти ее общее решение.
Две системы называются эквивалентными, если они имеют одно и то же общее решение.
№9 слайд
Содержание слайда: Система линейных уравнений называется однородной, если все свободные члены равны нулю:
Система линейных уравнений называется однородной, если все свободные члены равны нулю:
№10 слайд
Содержание слайда: 6.2. Решение невырожденных линейных систем. Формулы Крамера
Рассмотрим систему n линейных уравнений с n неизвестными
Данная система может быть записана в матричной форме:
№11 слайд
Содержание слайда: Основная матрица A такой системы квадратная. Определитель этой матрицы
Основная матрица A такой системы квадратная. Определитель этой матрицы
называется определителем системы.
Если определитель системы отличен от нуля, то система называется невырожденной.
№12 слайд
Содержание слайда: Решение системы трех уравнений с тремя неизвестными
Система трёх уравнений с тремя неизвестными имеет вид
№13 слайд
Содержание слайда: Определитель системы
№14 слайд
Содержание слайда: Система (2) может быть представлена в виде
Система (2) может быть представлена в виде
Откуда следует, что при система (2) имеет единственное решение, которое находится по формулам Крамера:
№15 слайд
Содержание слайда: При и хотя бы одном из
При и хотя бы одном из
отличном от нуля система (2) несовместна.
При
система (2) имеет бесчисленное множество решений.
№16 слайд
Содержание слайда: Пример
Решить систему по формулам Крамера
№17 слайд
Содержание слайда: Найдем определитель системы
Найдем определитель системы
№18 слайд
Содержание слайда: Вычислим
Вычислим
№19 слайд
Содержание слайда: По формулам Крамера находим
Ответ:
№20 слайд
Содержание слайда: 6.3. Исследование и решение СЛАУ. Теорема Кронекера-Капелли
Рассмотрим произвольную СЛАУ (1) содержащую m уравнений и n неизвестных.
Теорема 6.1. СЛАУ совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы:
№21 слайд
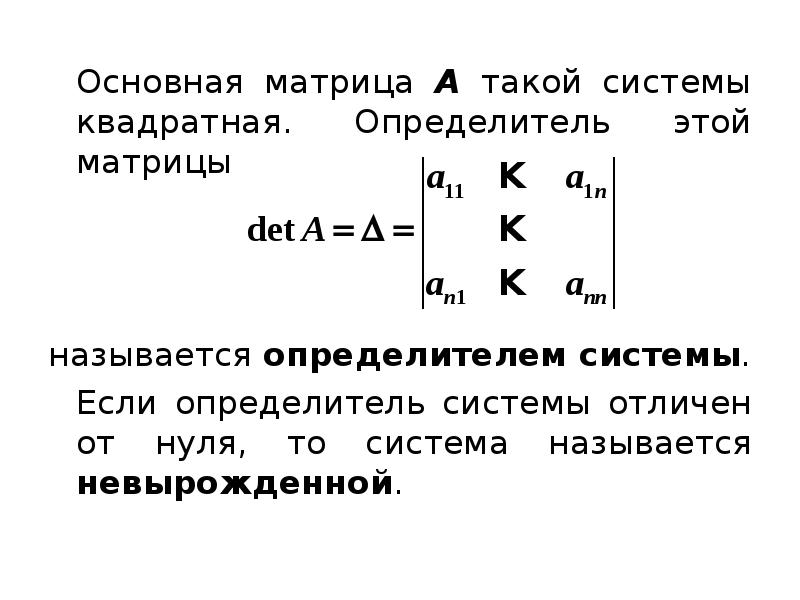
Содержание слайда: Теорема 6.2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Теорема 6.2. Если ранг совместной системы равен числу неизвестных, то система имеет единственное решение.
Если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений.
№22 слайд
Содержание слайда: 6.4. Метод Гаусса
Метод Гаусса (или метод последовательного исключения неизвестных) является универсальным методом решения систем линейных алгебраических уравнений.
№23 слайд
Содержание слайда: С помощью элементарных преобразований система уравнение приводится к равносильной системе ступенчатого вида, из которой последовательно, начиная с последних (по номеру) переменных находятся все остальные переменные.
С помощью элементарных преобразований система уравнение приводится к равносильной системе ступенчатого вида, из которой последовательно, начиная с последних (по номеру) переменных находятся все остальные переменные.
№24 слайд
Содержание слайда: Процесс решения по методу Гаусса состоит из двух этапов:
Процесс решения по методу Гаусса состоит из двух этапов:
На первом этапе (прямой ход) система приводится к ступенчатому виду.
На втором этапе (обратный ход) идет последовательное определение неизвестных из полученной ступенчатой системы.
№25 слайд
Содержание слайда: Элементарные преобразования
Перестановка уравнений местами.
Умножение какого-либо уравнения системы на число, отличное от нуля.
Умножение какого-либо уравнения системы на число, отличное от нуля и прибавление его к какому-либо уравнению системы.
№26 слайд
Содержание слайда: Рассмотрим метод Гаусса для системы третьего порядка, определитель которой не равен нулю:
Рассмотрим метод Гаусса для системы третьего порядка, определитель которой не равен нулю:
№27 слайд
Содержание слайда: Исключим из второго и третьего уравнений, используя элементарные преобразования системы а затем в полученной системе исключим из третьего уравнения. Мы приведем систему к «треугольному» виду:
Исключим из второго и третьего уравнений, используя элементарные преобразования системы а затем в полученной системе исключим из третьего уравнения. Мы приведем систему к «треугольному» виду:
№28 слайд
Содержание слайда: После этого начинается обратный ход метода Гаусса: из последнего уравнения находим , из второго - , из первого -
Замечание. Если коэффициент в системе равен нулю, то можно поменять местами уравнения или неизвестные.
№29 слайд
Содержание слайда: Рассмотренный метод решения, заключающийся в сведении исходной системы к системе, имеющей треугольный вид
называется методом Гаусса.
№30 слайд
Содержание слайда: Пример
Рассмотрим систему
№31 слайд
Содержание слайда: Исключим x из второго и третьего уравнения. Для этого первое уравнение умножим на –2 и сложим со вторым, затем первое уравнение умножим на –3 и сложим с третьим.
Исключим x из второго и третьего уравнения. Для этого первое уравнение умножим на –2 и сложим со вторым, затем первое уравнение умножим на –3 и сложим с третьим.
№32 слайд
Содержание слайда: Получим систему, равносильную данной:
Получим систему, равносильную данной:
Далее исключим y из третьего уравнения, для чего второе уравнение полученной системы умножим на –1 и сложим с третьим. Получим систему
№33 слайд
Содержание слайда: Из третьего уравнения подставим во второе
и найдем
Подставив найденные значения и
в первое уравнение
получим
Ответ:
№34 слайд
Содержание слайда: Пример
Решить систему методом Гаусса
Решение. Поменяем местами первое и второе уравнения системы (т. к. удобно иметь коэффициент при равный 1):
№35 слайд
Содержание слайда: Получим систему
Получим систему
Последнее равенство неверно. Следовательно, система несовместна.
Ответ:
№36 слайд
Содержание слайда: Пример
Решить систему методом Гаусса
Решение. Умножим первое уравнение на (-2) и сложим со вторым:
Таким образом, в системе остается одно уравнение
№37 слайд
Содержание слайда: Такая система имеет бесчисленное множество решений. Эти решения можно записать в виде:
№38 слайд
Содержание слайда: Пример
1. Установить, совместна ли система и, если она совместна, найти ее решение по формулам Крамера.
№39 слайд
Содержание слайда: Решение
Запишем систему в матричном виде:
№40 слайд
Содержание слайда: Определитель системы равен
Определитель системы равен
№41 слайд
Содержание слайда: Найденное решение - это точка пересечения прямых
Найденное решение - это точка пересечения прямых
и
№42 слайд
Содержание слайда: 2. Установить, совместна ли система и, если она совместна, найти ее решение по формулам Крамера.
2. Установить, совместна ли система и, если она совместна, найти ее решение по формулам Крамера.
Решение. Запишем систему в матричном виде:
№43 слайд
Содержание слайда: Определитель системы:
Определитель системы:
Определитель
отличен от нуля, следовательно система несовместна (т.е. не имеет решений).
№44 слайд
Содержание слайда: Так как каждое уравнение системы – это уравнение прямой и система не имеет решения, то это значит, что прямые
и
параллельны и не имеют общих точек.
№45 слайд
Содержание слайда: Тема: АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
№46 слайд
Содержание слайда: Линия на плоскости часто задается как множество точек, обладающих некоторым только им присущим геометрическим свойством.
Линия на плоскости часто задается как множество точек, обладающих некоторым только им присущим геометрическим свойством.
Замечание: геометрическим образом заданного уравнения не всегда является линия.
№47 слайд
Содержание слайда: ОПР. Уравнением линии (или кривой) на плоскости Оху называется такое уравнение с двумя переменными, которому удовлетворяют координаты x и y каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
ОПР. Уравнением линии (или кривой) на плоскости Оху называется такое уравнение с двумя переменными, которому удовлетворяют координаты x и y каждой точки линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
ОПР. Переменные x и y в уравнении линии называются текущими координатами точек линии.
№48 слайд
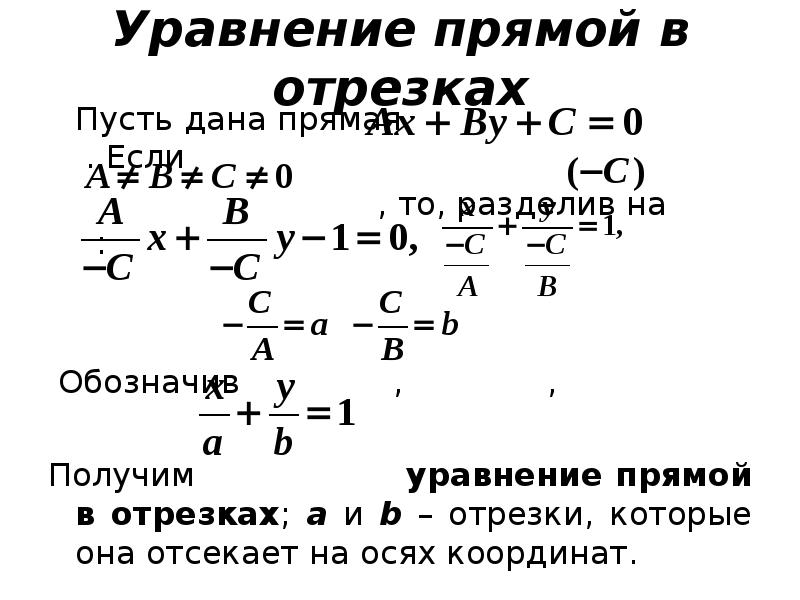
Содержание слайда: §1. Уравнения прямой на плоскости
Простейшей из линий является прямая.
Каждая прямая на плоскости OXY определяется уравнением первой степени с двумя неизвестными.
Обратно: каждое линейное уравнение первого порядка с двумя неизвестными определяет некоторую прямую на плоскости.
№49 слайд
Содержание слайда: 1.1. Различные виды уравнений прямой
Уравнение
называется общим уравнением прямой.
Каждая прямая на плоскости
определяется линейным уравнением первой степени с двумя неизвестными вида
и каждое линейное уравнение определяет некоторую прямую.
№50 слайд
Содержание слайда: Уравнение прямой в отрезках
Пусть дана прямая . Если
, то, разделив на :
Обозначив , ,
Получим уравнение прямой в отрезках; a и b – отрезки, которые она отсекает на осях координат.
№51 слайд
Содержание слайда: Пример
Записать уравнение прямой
в отрезках. Построить прямую.
Решение.
№52 слайд
Содержание слайда: Уравнение прямой с угловым коэффициентом k
Дана прямая , которая пересекает оси координат и не параллельна ни одной из них. Пусть угол наклона к положительному направлению оси Ox равен . Точка пересечения с Oy – .
№53 слайд
Содержание слайда:
№54 слайд
Содержание слайда: Пусть – произвольная точка прямой.
Пусть – произвольная точка прямой.
– уравнение прямой с угловым коэффициентом , где
Частные случаи:
1). – уравнение прямой, параллельной оси Ох и отстоящей от нее на ;
2). – прямая проходит через начало координат;
3). – уравнение оси Ox;
4). – уравнение оси Oy;
№55 слайд
Содержание слайда: Уравнение прямой, проходящей через данную точку
в данном направлении k
Пусть дана точка и задан угловой коэффициент k. Тогда уравнение прямой имеет вид:
№56 слайд
Содержание слайда: Уравнение прямой, проходящей через две
данные точки и
№57 слайд
Содержание слайда: Угол между прямыми
Рассмотрим на плоскости две прямые:
и
Пусть прямые пересекаются в точке M.
№58 слайд
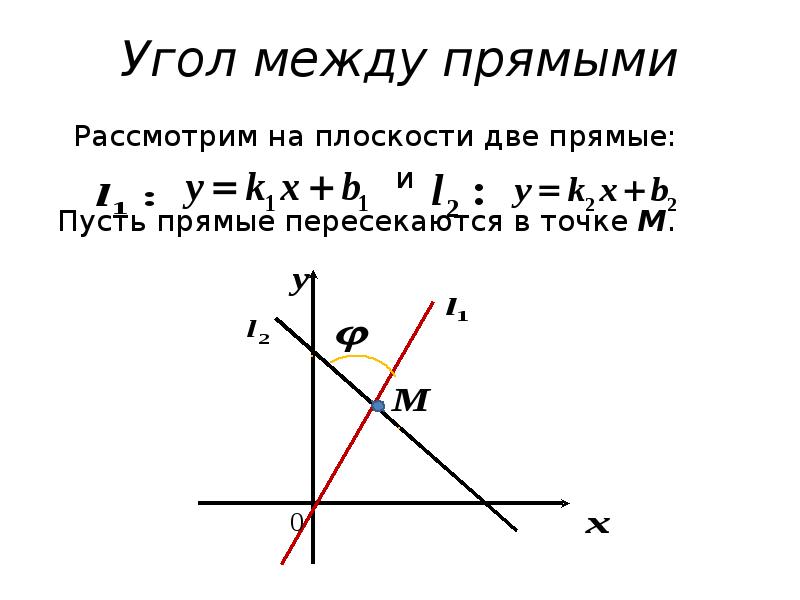
Содержание слайда: Углом между прямыми и будем называть наименьший угол, на который надо повернуть вокруг точки M против часовой стрелки до совпадения ее со второй прямой .
Углом между прямыми и будем называть наименьший угол, на который надо повернуть вокруг точки M против часовой стрелки до совпадения ее со второй прямой .
№59 слайд
Содержание слайда: Угол между прямыми:
Угол между прямыми:
Взаимное расположение двух прямых:
Прямые совпадают:
2. Прямые параллельны:
3. Перпендикулярны:
№60 слайд
Содержание слайда: Расстояние от точки до прямой
Расстояние d от точки до прямой
№61 слайд
Содержание слайда: Тема: Элементы векторной алгебры
№62 слайд
Содержание слайда: §1. Векторы
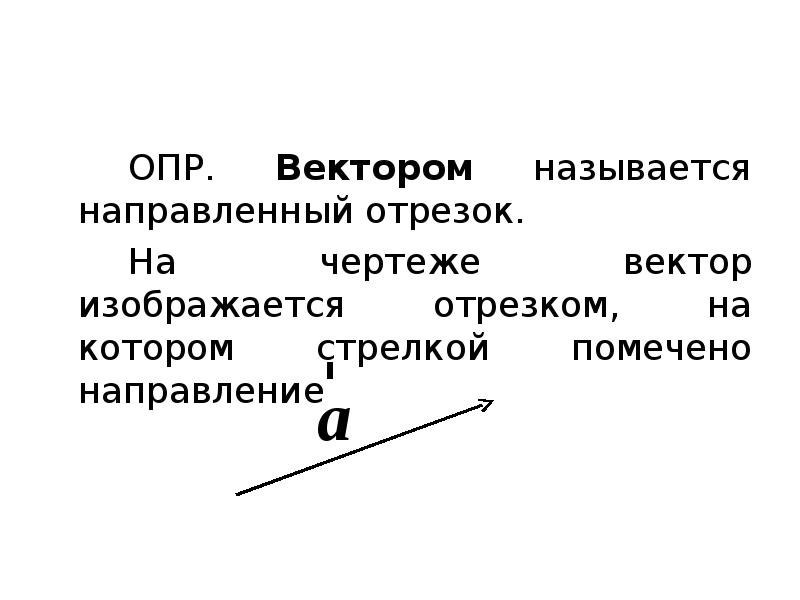
1.1. Основные понятия
Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.
Другие величины, например сила, скорость, ускорение, определяются не только своим числовым значением, но и направлением.
Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора.
№63 слайд
Содержание слайда: ОПР. Вектором называется направленный отрезок.
На чертеже вектор изображается отрезком, на котором стрелкой помечено направление
№64 слайд
Содержание слайда: Если один конец отрезка AB - точка A - начало вектора, а точка B - конец вектора, то вектор обозначается символом
Если один конец отрезка AB - точка A - начало вектора, а точка B - конец вектора, то вектор обозначается символом
№65 слайд
Содержание слайда: Расстояние между началом и концом вектора называется его модулем (или длиной). Модуль обозначается
Расстояние между началом и концом вектора называется его модулем (или длиной). Модуль обозначается
Вектор, начало и конец которого совпадают, называется нулевым вектором, обозначается . Модуль нулевого вектора равен 0, а направление не определено.
Вектор, длина которого равна единице, называется единичным (или ортом), обозначается
№66 слайд
Содержание слайда: Векторы, лежащие на параллельных прямых (или на одной прямой), называются коллинеарными
Векторы, лежащие на параллельных прямых (или на одной прямой), называются коллинеарными
Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
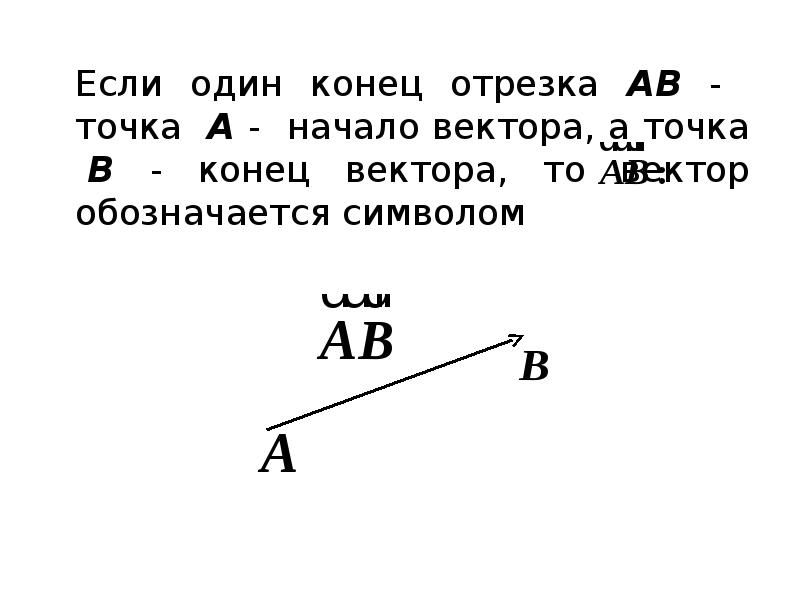
№67 слайд
Содержание слайда: Два коллинеарных вектора называются противоположными, если они имеют равные модули и противоположное направление. Вектор, противоположный вектору , обозначается
Два коллинеарных вектора называются противоположными, если они имеют равные модули и противоположное направление. Вектор, противоположный вектору , обозначается
№68 слайд
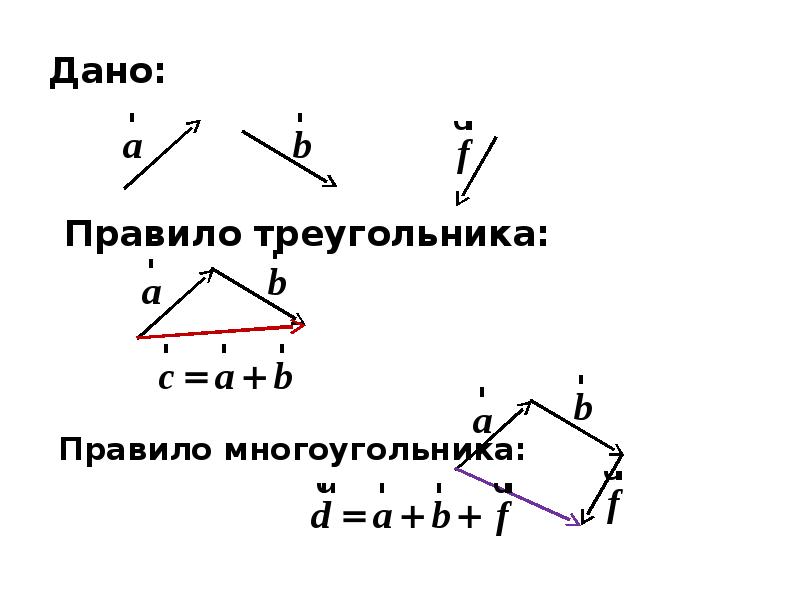
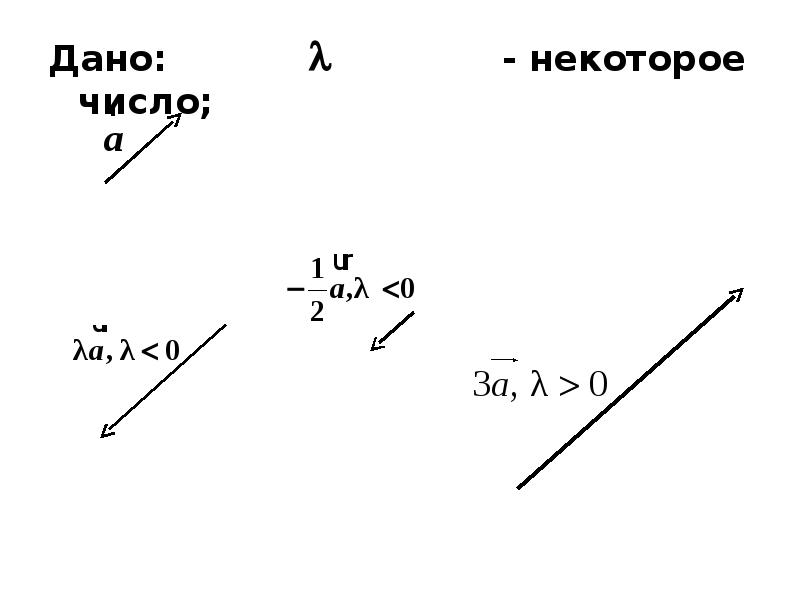
Содержание слайда: 1.2. Линейные операции над векторами
Линейными операциями над векторами называют их сложение, вычитание, умножение вектора на число.
Суммой двух векторов и называется вектор , начало которого совпадает с началом вектора , а конец ― с концом вектора , при условии, что начало вектора совмещено с концом вектора .
Записывают
№69 слайд
Содержание слайда: Дано:
Дано:
№70 слайд
Содержание слайда: Умножение вектора на число
Произведением вектора на число
называется вектор , который удовлетворяет условиям:
1)
и ― одинаково направлены при
и ― противоположно направлены при
№71 слайд
Содержание слайда: Дано: - некоторое число;
Дано: - некоторое число;
№72 слайд
Содержание слайда: 1.3. Проекция вектора на ось
Пусть в пространстве задана ось т. е. направленная прямая.
№73 слайд
Содержание слайда: Если точка M лежит на оси, то ее проекция на ось совпадает с самой точкой.
Если точка M лежит на оси, то ее проекция на ось совпадает с самой точкой.
Пусть — произвольный вектор. Обозначим через и проекции на ось соответственно начала и конца вектора и рассмотрим вектор
ОПР. Проекцией вектора на ось называется положительное число , если вектор и ось одинаково направлены и отрицательное число
если вектор и ось противоположно направлены.
№74 слайд
Содержание слайда: Если точки и совпадают, то проекция вектора равна 0.
Если точки и совпадают, то проекция вектора равна 0.
Проекция вектора на ось обозначается: пр
Угол между вектором и осью (или угол между двумя векторами) изображен на рисунке
№75 слайд
Содержание слайда: 1.4. Линейная зависимость векторов
При решении различных задач, как правило, приходится иметь дело не с одним вектором, а с некоторой совокупностью векторов одной размерности. Такую совокупность векторов называют системой векторов и обозначают:
№76 слайд
Содержание слайда: ОПР. Линейной комбинацией векторов (1) называется вектор вида
ОПР. Линейной комбинацией векторов (1) называется вектор вида
где – любые действи-тельные числа. В этом случае говорят также, что вектор линейно выражается через векторы
№77 слайд
Содержание слайда: ОПР. Система ненулевых векторов (1) называется линейно зависимой, если существую такие числа , не равные одновременно нулю, что линейная комбинация данной системы с указанными числами равна нулевому вектору:
ОПР. Система ненулевых векторов (1) называется линейно зависимой, если существую такие числа , не равные одновременно нулю, что линейная комбинация данной системы с указанными числами равна нулевому вектору:
Если же равенство (2) для данной системы векторов выполняется лишь при
то такая система векторов называется линейно независимой.
№78 слайд
Содержание слайда: ОПР. Размерностью системы векторов называется максимальное число содержащихся в нем линейно независимых векторов.
ОПР. Размерностью системы векторов называется максимальное число содержащихся в нем линейно независимых векторов.
Если таких векторов n, то система называется n-мерной.
ОПР. Совокупность n линейно независимых векторов n -мерной системы векторов (1) называется ее базисом.
№79 слайд
Содержание слайда: Теорема Каждый вектор n-мерной системы векторов можно представить и притом единственным способом в виде линейной комбинации векторов базиса
Теорема Каждый вектор n-мерной системы векторов можно представить и притом единственным способом в виде линейной комбинации векторов базиса
Равенство (3) называется разложением вектора по базису а числа – координатами вектора относительно этого базиса.
№80 слайд
Содержание слайда: В силу единственности разложения (3) каждый вектор однозначно может быть определен координатами в некотором базисе.
В силу единственности разложения (3) каждый вектор однозначно может быть определен координатами в некотором базисе.
На плоскости любые два неколлинеарных вектора образуют базис.
В пространстве любые три некомпланарных вектора образуют базис.
№81 слайд
Содержание слайда: 1.5. Координаты вектора
Координатами вектора в прямоугольной системе координат OXY называются проекции x, y, вектора на оси координат. Обозначают
№82 слайд
Содержание слайда: Множество всех n-мерных векторов с действительными координатами обозначается
Таким образом, вектор
№83 слайд
Содержание слайда: Если , – единичные векторы (орты) координатных осей, то вектор можно представить в виде
Если , – единичные векторы (орты) координатных осей, то вектор можно представить в виде
Направляющими косинусами вектора
называются косинусы углов , , образуемых им с осями координат OX и OY соответственно.
№84 слайд
Содержание слайда: Если вектор имеет начало в точке
Если вектор имеет начало в точке
и конец в точке , то координаты вектора равны разности соответствую-щих координат конечной и начальной его точек:
Модуль вектора
№85 слайд
Содержание слайда: Пример
Даны точки и
Найти: а) координаты
б) модуль
Решение. а) Координаты
б) Модуль найдем, используя формулу
№86 слайд
Содержание слайда: 1.6. Действия над векторами, заданными координатами
Пусть
тогда
№87 слайд
Содержание слайда: Условие параллельности векторов и
Условие параллельности векторов и
Условие перпендикулярности векторов
и
№88 слайд
Содержание слайда: 1.7. Скалярное произведение векторов
ОПР. Скалярным произведением векторов
и называется число, равное произве-дению их модулей на косинус угла между ними:
Если известны координаты векторов и
то скалярное произведение можно вычислить по формуле
№89 слайд
Содержание слайда: Свойства скалярного произведения:
1).
2).
3).
4).
№90 слайд
Содержание слайда: Угол между векторами:
Условие перпендикулярности векторов:
если и ― ненулевые векторы.
№91 слайд
Содержание слайда: Пример
Найти скалярное произведение векторов
И , если угол между ними равен 60°,
Решение. Так как
то
№92 слайд
Содержание слайда: Рассмотрим пространство
Рассмотрим пространство
Вектор
Тогда
№93 слайд
Содержание слайда: Компланарность векторов
Три вектора
компланарны тогда и только тогда, когда
Скачать все slide презентации Высшая математика. Учебно-методическое пособие для подготовки к компьютерному тестированию. 2 семестр одним архивом:
