Презентация Понятие квадратного корня из неотрицательного числа онлайн
На нашем сайте вы можете скачать и просмотреть онлайн доклад-презентацию на тему Понятие квадратного корня из неотрицательного числа абсолютно бесплатно. Урок-презентация на эту тему содержит всего 9 слайдов. Все материалы созданы в программе PowerPoint и имеют формат ppt или же pptx. Материалы и темы для презентаций взяты из открытых источников и загружены их авторами, за качество и достоверность информации в них администрация сайта не отвечает, все права принадлежат их создателям. Если вы нашли то, что искали, отблагодарите авторов - поделитесь ссылкой в социальных сетях, а наш сайт добавьте в закладки.
Оцените презентацию от 1 до 5 баллов!
- Тип файла:ppt / pptx (powerpoint)
- Всего слайдов:9 слайдов
- Для класса:1,2,3,4,5,6,7,8,9,10,11
- Размер файла:778.50 kB
- Просмотров:212
- Скачиваний:1
- Автор:неизвестен
Слайды и текст к этой презентации:
№1 слайд
Содержание слайда:
№2 слайд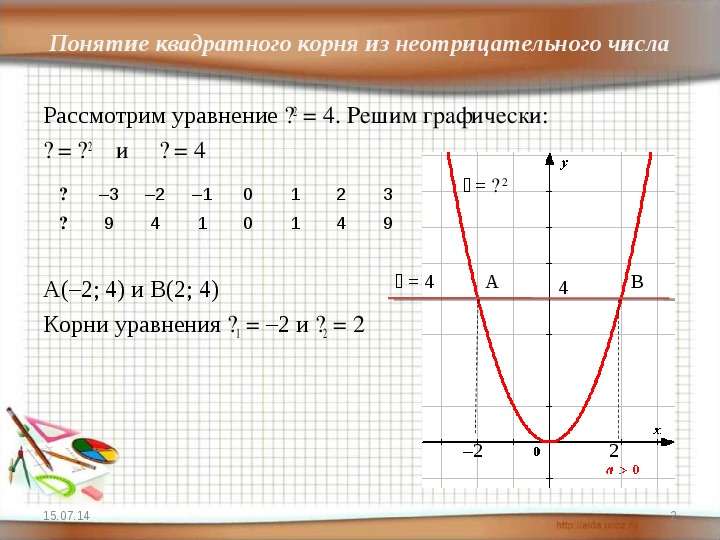
Содержание слайда: Рассмотрим уравнение ��2 = 4. Решим графически:
Рассмотрим уравнение ��2 = 4. Решим графически:
�� = �� 2 и �� = 4
А(–2; 4) и В(2; 4)
Корни уравнения ��1 = –2 и ��2 = 2
№3 слайд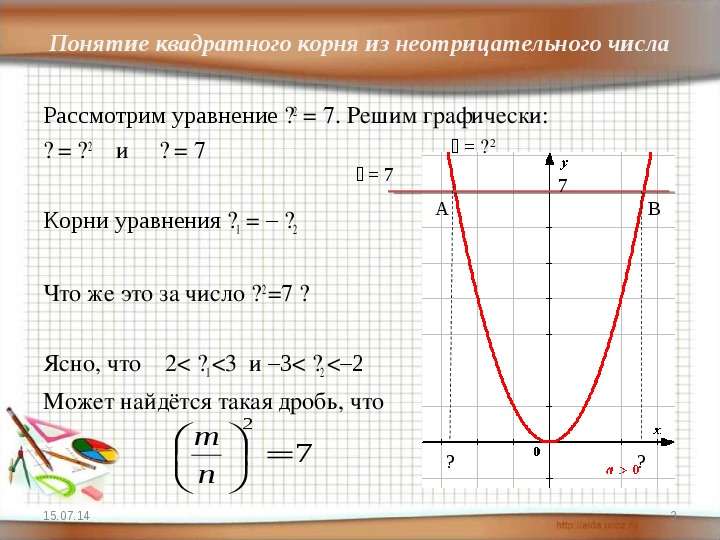
Содержание слайда: Рассмотрим уравнение ��2 = 7. Решим графически:
Рассмотрим уравнение ��2 = 7. Решим графически:
�� = �� 2 и �� = 7
Корни уравнения ��1 = – ��2
Что же это за число �� 2 =7 ?
Ясно, что 2< ��1 <3 и –3< ��2 <–2
Может найдётся такая дробь, что
№4 слайд
Содержание слайда: Оказывается такой дроби нет! (смотри доказательство утверждения в учебнике!)
Оказывается такой дроби нет! (смотри доказательство утверждения в учебнике!)
Встретившись с подобной ситуацией, математики поняли, что надо придумать способ её описания на математическом языке.
Они ввели в рассмотрение новый символ и с его помощью корни уравнения ��2 = 7 записали так:
��1 = ��2 = –
№5 слайд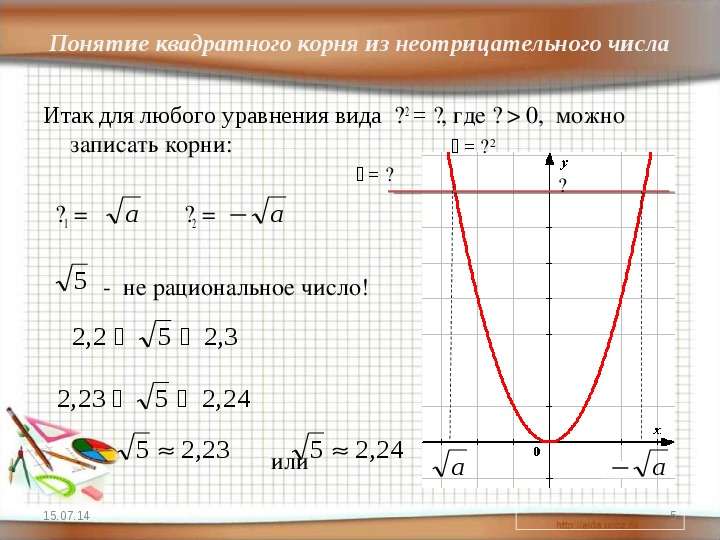
Содержание слайда: Итак для любого уравнения вида �� 2 = ��, где �� > 0, можно записать корни:
Итак для любого уравнения вида �� 2 = ��, где �� > 0, можно записать корни:
��1 = ��2 =
- не рациональное число!
или
№6 слайд
Содержание слайда: Определение: Квадратным корнем из неотрицательного числа �� называют такое неотрицательное число, квадрат которого равен ��.
Определение: Квадратным корнем из неотрицательного числа �� называют такое неотрицательное число, квадрат которого равен ��.
, где �� – называют подкоренным числом
Итак, если �� – неотрицательное число, то:
1)
2)
Если �� < 0, то уравнение ��2 = �� не имеет корней
Если �� = 0, то уравнение ��2 = �� имеет один корень ��1= 0
Если �� > 0, то уравнение ��2 = �� имеет два корня
��1 = ��2 =
№7 слайд
Содержание слайда: Равенство и ��2 = �� выражают одну и ту же зависимость между неотрицательными числами �� и ��, но только вторая описана на более простом языке, чем первая.
Равенство и ��2 = �� выражают одну и ту же зависимость между неотрицательными числами �� и ��, но только вторая описана на более простом языке, чем первая.
Операцию по нахождению квадратного корня из неотрицательного числа называют извлечением квадратного корня.
Эта операция является обратной по отношению к возведению в квадрат.
№8 слайд
Содержание слайда: Примеры:
Примеры:
= 5, так как 5>0 и 52 = 25
= 15 , так как 15>0 и 152 = 225
= 9 , так как 9>0 и 92 = 81
= , так как >0 и =
= 31 , так как 31>0 и 312 = 961
= не существует!
≈ 3,16
№9 слайд
Содержание слайда: Определение: Кубическим корнем из неотрицательного числа �� называют такое неотрицательное число, куб которого равен ��.
Определение: Кубическим корнем из неотрицательного числа �� называют такое неотрицательное число, куб которого равен ��.
т. е.
Пример:
= 3, т.к. 3>0 и 33 = 27
= 5, т.к. 5>0 и 53 = 125
Скачать все slide презентации Понятие квадратного корня из неотрицательного числа одним архивом:
