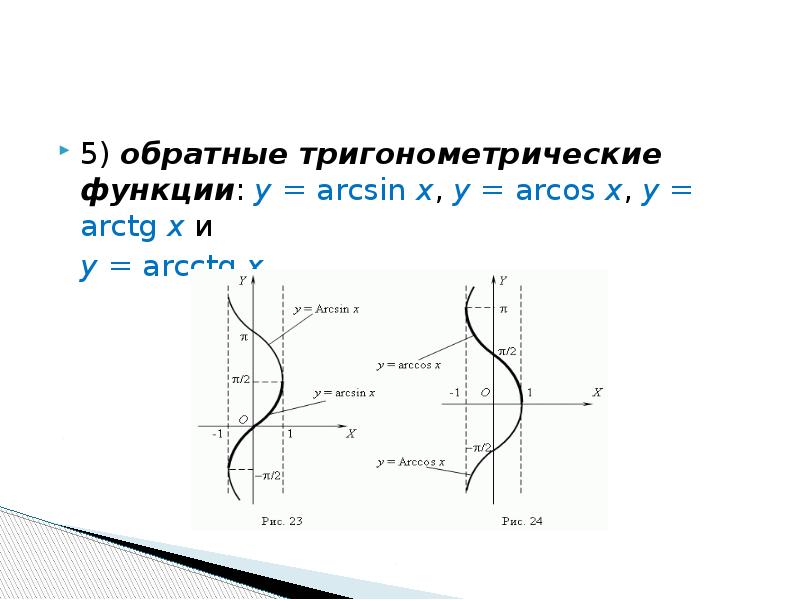
Презентация Функции и их свойства. Графики функций. Предел функции. Непрерывность функции онлайн
На нашем сайте вы можете скачать и просмотреть онлайн доклад-презентацию на тему Функции и их свойства. Графики функций. Предел функции. Непрерывность функции абсолютно бесплатно. Урок-презентация на эту тему содержит всего 62 слайда. Все материалы созданы в программе PowerPoint и имеют формат ppt или же pptx. Материалы и темы для презентаций взяты из открытых источников и загружены их авторами, за качество и достоверность информации в них администрация сайта не отвечает, все права принадлежат их создателям. Если вы нашли то, что искали, отблагодарите авторов - поделитесь ссылкой в социальных сетях, а наш сайт добавьте в закладки.
Презентации » Образование » Функции и их свойства. Графики функций. Предел функции. Непрерывность функции
Оцените!
Оцените презентацию от 1 до 5 баллов!
- Тип файла:ppt / pptx (powerpoint)
- Всего слайдов:62 слайда
- Для класса:1,2,3,4,5,6,7,8,9,10,11
- Размер файла:463.83 kB
- Просмотров:94
- Скачиваний:0
- Автор:неизвестен
Слайды и текст к этой презентации:
№1 слайд


Содержание слайда: ВОЕННО–МЕДИЦИНСКАЯ АКАДЕМИЯ
имени С.М. Кирова
Кафедра биологической и медицинской физики
ЛЕКЦИЯ № 1
по дисциплине «Математика»
на тему: «Функции и их свойства. Графики функций. Предел функции. Непрерывность функции»
для курсантов I курса по военной специальности «Фармация»
№6 слайд


Содержание слайда: Определение:
Пусть X, У — некоторые множества, элементами которых являются некоторые числа. Если каждому числу х Є X по некоторому закону или правилу f ставится в соответствие число у Є У, то говорят, что на множестве X задана числовая функция f и записывают эту функциональную зависимость формулой
у = f(x).
№10 слайд


Содержание слайда: а) конечные промежутки:
Открытый интервал (a,b): множество вещественных чисел, удовлетворяющих неравенствам a < x < b или (a,b) ↔ (a < x < b), где знак эквивалентности;
Замкнутый интервал (или отрезок) [a,b]: [a,b] ↔ (a≤ x ≤ b);
Полуоткрытые интервалы (a,b] и [a,b): (a,b] ↔ (a< x ≤ b) или [a,b) ↔ (a≤ x < b).
№13 слайд


Содержание слайда: Способы задания функции:
1) Графический.
Правило, по которому можно находить у, зная х, может быть задано графиком функции.
Графиком функции в декартовой прямоугольной системе координат называется множество всех точек, абсциссы которых являются значениями аргумента, а ординаты - соответствующими значениями функции.
№15 слайд


Содержание слайда: Функцию можно задавать также с помощью таблицы или формулы (аналитически).
2) Табличный способ применяется на практике при обработке результатов наблюдений приближенных значений функции.
3) Аналитический способ задания функции является наиболее удобным для полного исследования функции при помощи методов математического анализа.
№17 слайд


Содержание слайда: Определение. Функция называется возрастающей (убывающей) в интервале, если большему значению аргумента из этого интервала соответствует большее (меньшее) значение функции.
График возрастающей на интервале (а,b) функции, если его рассматривать слева направо, поднимается вверх, а для убывающей функции — опускается вниз.
№19 слайд


Содержание слайда: Определение. Интервал независимой переменной, в котором функция возрастает (убывает), называется интервалом возрастания (убывания). Как интервал возрастания, так и интервал убывания называют интервалами монотонности функции, а функцию в этом интервале — монотонной функцией.
№21 слайд


Содержание слайда: Таким образом, если функция f(x) — четная, то для всех х из ее области определения должно выполняться равенство f(-x)=f(x), как это происходит, например, при f(x) = x2, а если f(x) — нечетная, то f(-x) = -f(x) для любого х из области определения функции, как, например, в случае f(x)= x3.
№24 слайд


Содержание слайда: Определение.
Функция f(x) называется периодической, если существует такое положительное число а, что f(x + a) = f(x) = f(x - а) для любого х из ООФ (точки х, х + а, х -а относятся к области определения функции).
При этом наименьшее положительное а с таким свойством (если таковое существует) называется периодом функции.
№27 слайд


Содержание слайда: Определение. Сложной функцией называется функция, аргумент которой также является функцией, т.е. F(x) = f(φ(x)).
Чтобы сосчитать значение в точке х сложной функции f(φ(x)), составленной из функций f и φ, следует сначала найти частное значение u= φ(х) внутренней функции φ, а затем подставить его в качестве аргумента во внешнюю функцию f.
№30 слайд


Содержание слайда: Обратная функция
Рассмотрим функцию с областью определения X и областью значений Y. Предположим, что каждому значению у ε Y соответствует одна определенная точка
х ε X, такая что у = f(x). Тогда существует функция φ, переводящая любое у ε Y
в х ε X, удовлетворяющее вышеуказанному свойству у = f(x).
№42 слайд


Содержание слайда: 4. Предел функции. Основные теоремы о пределах. Специальные пределы
Пример. Пусть задана функция
f(x) = ,
определенная при всех значениях х, кроме
х = 1.
(Отметим, что эта функция не эквивалентна функции f(x) = x +1, получаемой при сокращении правой части на х – 1, так как эти функции имеют разные области определения).
№45 слайд


Содержание слайда: Определение. Пусть функция f(x) определена в некоторой окрестности точки x0, кроме, может быть, самой точки x0.
Число b называется пределом функции в точке x0 (или при х → x0), если для любого положительного ε, как бы мало оно не было, можно найти такое положительное δ, что для всех x ≠ x0, удовлетворяющих неравенству |x - x0| < δ, выполняется неравенство |f(x) - b | <ε.
Записывают так: lim f(x) = b.
x→x0
№47 слайд


Содержание слайда: Теорема 1 (о единственности предела функции). Функция не может иметь более одного предела.
Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки x0, за исключением, может быть, самой точки x0, то либо они имеют один и тот же предел при x → x0, либо обе не имеют предела в этой точке.
№55 слайд


Содержание слайда: 5. Непрерывность функций
Рассмотрим функцию у = f(х), определенную в интервале [а, b].
Пусть х0 и х — два произвольных значения из этого интервала. Обозначим х -х0 = Δх, откуда х = х0 + Δх.
Говорят, что для перехода от значения аргумента х0 к значению х первоначальному значению придано приращение Δх.
№59 слайд


Содержание слайда: Непрерывность функции в точке x0 равносильна ее непрерывности в этой точке одновременно слева и справа, то есть должны выполняться следующие четыре условия непрерывности:
1. f(x) должна быть определена в некоторой окрестности точки x0.
2. Должны существовать конечные пределы слева и справа:
lim f(x) и lim f(x)
x→x0-0 x→x0+0
3. Эти пределы слева и справа должны быть равны:
lim f(x) = lim f(x) = А
x→x0-0 x→x0+0
4. Эти пределы должны быть равны значению функции в точке x0, т. е. А = f(x0).
№60 слайд


Содержание слайда: Если в точке x0 не выполняется хотя бы одно условие, то в этой точке функция терпит разрыв, а сама эта точка называется точкой разрыва.
В качестве конкретного примера функции, имеющей точку разрыва, рассмотрим изменение биомассы микроорганизмов, чувствительных к температурным колебаниям.
№62 слайд


Содержание слайда: Классификация точек разрыва
Пусть x0 является внутренней точкой отрезка [а, b]. Если существуют конечные пределы f(x) при стремлении x к x0 слева и справа, но нарушены условия 3 или 4, то точку x0 называют точкой разрыва первого рода.
Если хотя бы один из пределов слева или справа бесконечен или его вовсе нет, тогда говорят о разрыве второго рода.
Скачать все slide презентации Функции и их свойства. Графики функций. Предел функции. Непрерывность функции одним архивом:
Похожие презентации
-
 Свойства функций, имеющих предел. Асимптоты графика функции и методы их отыскания.
Свойства функций, имеющих предел. Асимптоты графика функции и методы их отыскания. -
 На тему Графики функций синуса и косинуса и их свойства
На тему Графики функций синуса и косинуса и их свойства -
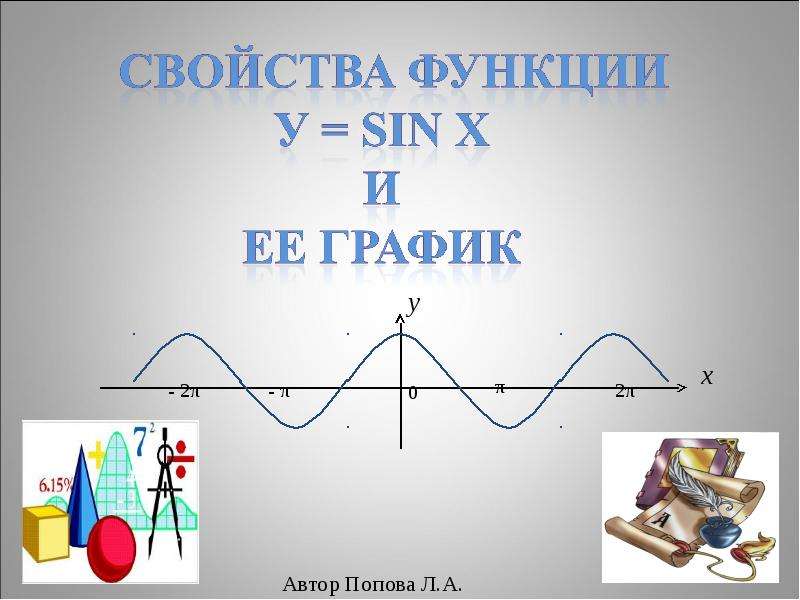 Свойства функции У sin x и ее график
Свойства функции У sin x и ее график -
 Пределы. Непрерывность функций
Пределы. Непрерывность функций -
 Показательная функция, ее свойства и график
Показательная функция, ее свойства и график -
 Функция y cos x. Ее свойства и график
Функция y cos x. Ее свойства и график -
 Показательная функция, ее свойства и график 11 класс
Показательная функция, ее свойства и график 11 класс -
 ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ.
ПРЕДЕЛ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ. -
 Определение непрерывности функции в точке
Определение непрерывности функции в точке -
 Свойства функции и их графики
Свойства функции и их графики