Презентация ВВЕДЕНИЕ В БАЙЕСОВСКИЕ СЕТИ Алгоритмы для Интернета, ИТМО & СПбГУ С. -Петербург, 26 октября 2006 Рук. семинара Ю. М. Лифшиц онлайн
На нашем сайте вы можете скачать и просмотреть онлайн доклад-презентацию на тему ВВЕДЕНИЕ В БАЙЕСОВСКИЕ СЕТИ Алгоритмы для Интернета, ИТМО & СПбГУ С. -Петербург, 26 октября 2006 Рук. семинара Ю. М. Лифшиц абсолютно бесплатно. Урок-презентация на эту тему содержит всего 184 слайда. Все материалы созданы в программе PowerPoint и имеют формат ppt или же pptx. Материалы и темы для презентаций взяты из открытых источников и загружены их авторами, за качество и достоверность информации в них администрация сайта не отвечает, все права принадлежат их создателям. Если вы нашли то, что искали, отблагодарите авторов - поделитесь ссылкой в социальных сетях, а наш сайт добавьте в закладки.
Презентации » Авто/мото » ВВЕДЕНИЕ В БАЙЕСОВСКИЕ СЕТИ Алгоритмы для Интернета, ИТМО & СПбГУ С. -Петербург, 26 октября 2006 Рук. семинара Ю. М. Лифшиц
Оцените!
Оцените презентацию от 1 до 5 баллов!
- Тип файла:ppt / pptx (powerpoint)
- Всего слайдов:184 слайда
- Для класса:1,2,3,4,5,6,7,8,9,10,11
- Размер файла:6.44 MB
- Просмотров:145
- Скачиваний:0
- Автор:неизвестен
Слайды и текст к этой презентации:
№6 слайд


Содержание слайда: Уточнение-2
…В частности, мы предполагаем, что можем производить (пользуясь, например, «грубой силой», т.е. подходом по определению) любые желаемые операции, такие, как маргинализацию или нормировку, внутри любой клики, но необязательно непосредственно для всей сети сразу…
№14 слайд


Содержание слайда: Почему БС востребованы
ИИ (МВ): знания с неопределенностью, фрагменты знаний, базы фрагментов знаний
Статистика: много переменных, связи всех со всеми неописуемые и неоцениваемые, зато отдельные скопления можно неплохо охарактеризовать
Техника: декомпозируемость систем, знание свойств элементов и связей между ними
№21 слайд


Содержание слайда: Немного об истории
Логика (от Аристотеля и раньше);
Вероятностная логика (от Дж. Буля и позже); в ИИ удачно ввел Н. Нильссон в 1986; различные формализации, мы пользуемся Хальперном, Фагином и Меггиддо;
Байесовские сети (БСД – Дж. Пиэрл, АБС – В.И. Городецкий), еще и марковские сети (???);
история этим не исчерпывается; смежные дисциплины...
№22 слайд


Содержание слайда: Немного об особенностях
Очень большой упор на графическое представление отношений независимости и условной независимости.
Стремление избежать обсуждения тех проблем, решения которых они не знают (подмена циклов последовательностью фрагментов знаний, …)
А нам бы о представлении данных хотелось бы поговорить побольше, непротиворечивость посмотреть, алгоритмы вывода выписать и сделать понятными, на доступные программные технологии опереться.
№23 слайд


Содержание слайда: БСД: литература
Статьи
Pearl J. (1985). How to Do with Probabilities what People Say You Can't. Artificial Intelligence Applications. Ed. Weisbin C.R., IEEE, North Holland, pp. 6--12.
Pearl J. (1986). Fusion, Propagation, and Structuring in Belief Networks. Artificial Intelligence, vol. 29. Elsevier Science Publishers B.V., North Holland, pp. 241--288.
Pearl J. (1986a). Constraint-Propagation Approach to Probabilistic Reasoning. Machine Intelligence & Pattern Recognition (Uncertainty in Artificial Intelligence). Eds. Kanal L.N., Lemmer J.F. Vol. 4, Elsevier Science Publishers B.V., North Holland, pp. 357--369.
Pearl J. (1986b). On Evidentional Reasoning in Hierarchy of Hypotheses. Artificial Intelligence, vol. 28. Elsevier Science Publishers B.V., North Holland, pp. 9--15.
Pearl J. (1986c). Distributed Revision of Composite Beliefs. Artificial Intelligence, vol. 33. Elsevier Science Publishers B.V., North Holland, pp. 173--215.
Монографии
Pearl J. (1988). Probabilistic Reasoning in Intelligent Systems. Morgan Kaufmann Publishers, 552 pp.
Pearl J. (2000). Causality: Models, Reasoning, and Inference. Cambridge University Press, 386 pp.
Jensen F.V.(2001). Bayesian Networks and Decision Graphs. Springer-Verlag, NY. 268 pp.
Korb K.B., Nicholson A.E. (2004). Bayesian Artificial Intelligence. Chapman and Hall/CRC, 364 pp.
Kyburg H.E. Jr. (2001). Uncertain Inference. Cambridge University Press, 298 pp.
Lauritzen, S. L. (1996). Graphical Models, Oxford University Press, Oxford, 1996.
Neapolitan R.E. (2004). Learning Bayesian Networks. Pearson Prentice Hall, 674 pp.
Nilsson N.J. (1998). Artificial Intelligence: A New Synthesis. Morgan Kaufmann Publishers, 514 pp.
№24 слайд


Содержание слайда: АБС: литература
Gorodetsky V.I., Drozdgin V.V., Jusupov R.M. Application of Attributed Grammar and Algorithmic Sensitivity Model for Knowledge Representation and Estimation // Artificial Intelligence and Information, Control Systems of ROBOTSA. North Holland, Elsevier Science Publ., 1984. pp. 232--237.
Городецкий В.И. Байесовский вывод. АН СССР, ЛИИАН, Препринт № 149. Л., 1991.
Городецкий В.И. Алгебраические байесовские сети --- новая парадигма экспертных систем // Юбилейный сборник трудов институтов Отделения информатики, вычислительной техники и автоматизации Российской Академии наук, т. 2. М., РАН, 1993. с. 120--141.
Городецкий В.И., Тулупьев А.Л. Формирование непротиворечивых баз знаний с неопределенностью // Известия РАН. Серия "Теория и системы управления». 1997. №5.
Тулупьев А.Л. Алгебраические байесовские сети. Теоретические основы и непротиворечивость. СПб.: СПИИРАН, 1995. 76 с.
Тулупьев А.Л. Алгебраические байесовские сети. Логико-вероятностный подход к моделированию баз знаний с неопределенностью. СПб.: СПИИРАН, 2000. 292 с.
Тулупьев А.Л., Николенко С.И., Сироткин А.В. Байесовские сети: логико-вероятностный подход. СПб.: Наука, 2006. 607 с.
№38 слайд


Содержание слайда: Вероятность истинности
Подход по Н. Нильссону (1986 г.)
Более глубокая формализация дана в работах коллектива Фагина, Хальперна, Миггидо (пригодна для рассуждений об оценках сложности)
Другие глубокие формализации
Спор о приоритетах (de Finetti…)
Дж. Буль --- тоже писал о вероятности пропозиции
№64 слайд
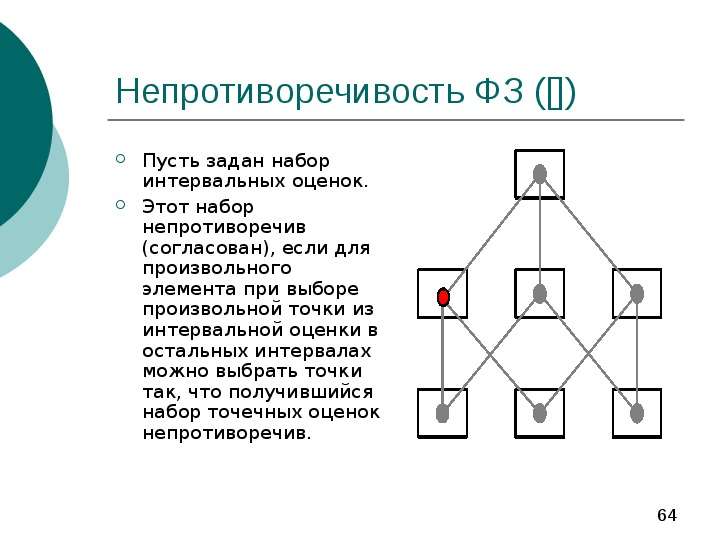

Содержание слайда: Непротиворечивость ФЗ ([])
Пусть задан набор интервальных оценок.
Этот набор непротиворечив (согласован), если для произвольного элемента при выборе произвольной точки из интервальной оценки в остальных интервалах можно выбрать точки так, что получившийся набор точечных оценок непротиворечив.
№85 слайд


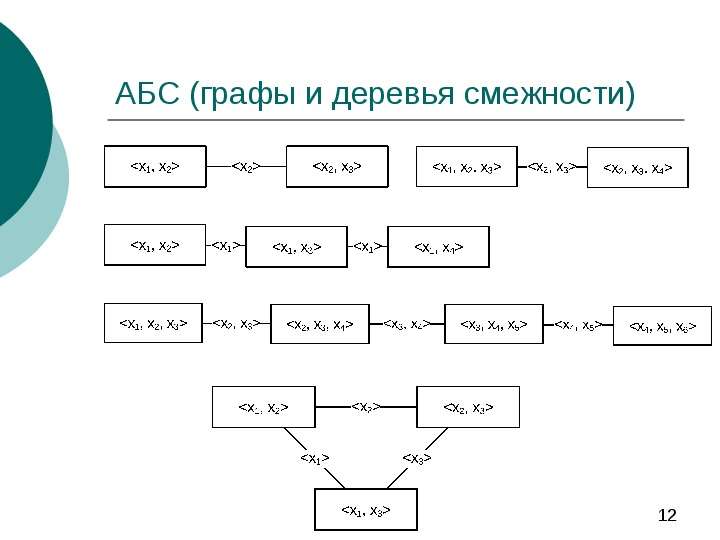
Содержание слайда: Граф смежности --- определение
Графом смежности называется ненаправленный граф, в котором
между каждой парой узлов, веса которых содержат общие элементы, существует путь;
в веса каждого из узлов любого пути (в графе) входят все элементы, общие для начального и конечного узлов этого пути;
вес одного узла не входит полностью в вес никакого другого узла.
№111 слайд


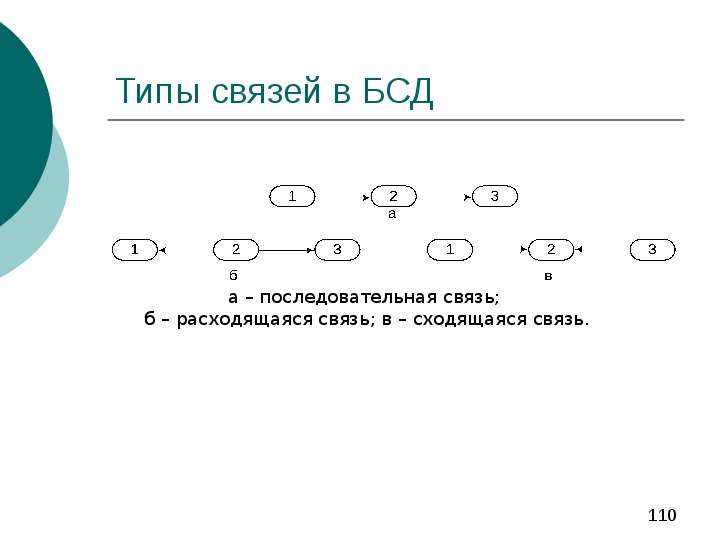
Содержание слайда: Понятие d-разделимости
Два узла называются
d-разделимыми, если любой путь между ними содержит последовательную или сходящуюся связь, в центральный узел которой поступило свидетельство, или расходящуюся связь, в центральный узел (и его потомки) которой не поступило свидетельство.
№114 слайд


Содержание слайда: Что нам дают такие предположения
Независимость d-разделимых [переменных в узлах] позволяет выделить единственное распределение из всех, для которых подходят заданные условные вероятности.
Это единственное распределение -- произведение всех вероятностей, заданных в БСД (chain rule).
№119 слайд


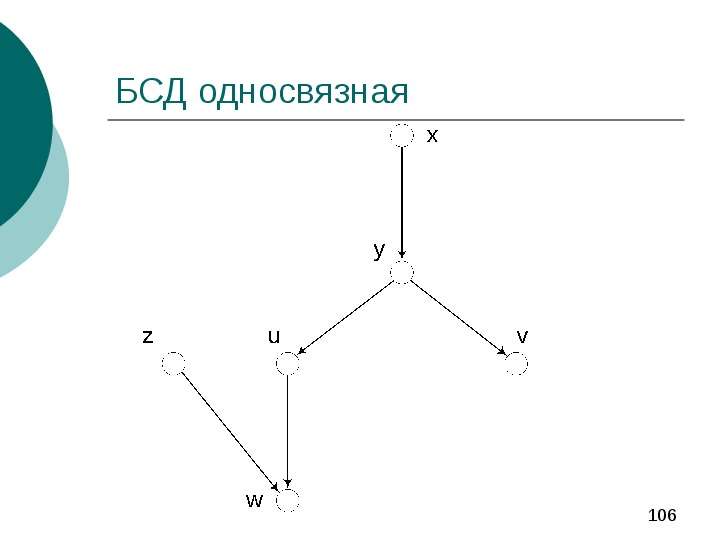
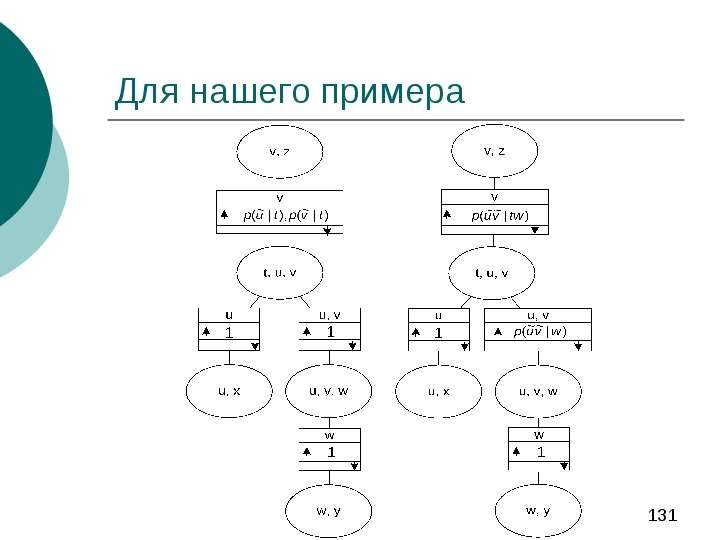
Содержание слайда: Алгоритм первичной пропагации для ациклических направленных графов
Очевидно, что в описанном выше примере нам в ходе вычисления p(w) потребуются вероятности
именно в такой ситуации и требуется chain rule и понятие d-разделимости.
В частности получаем, что
p(uv|t) = p(u|t) × p(v|t),
аналогично для отрицания t и суммируем.
№120 слайд


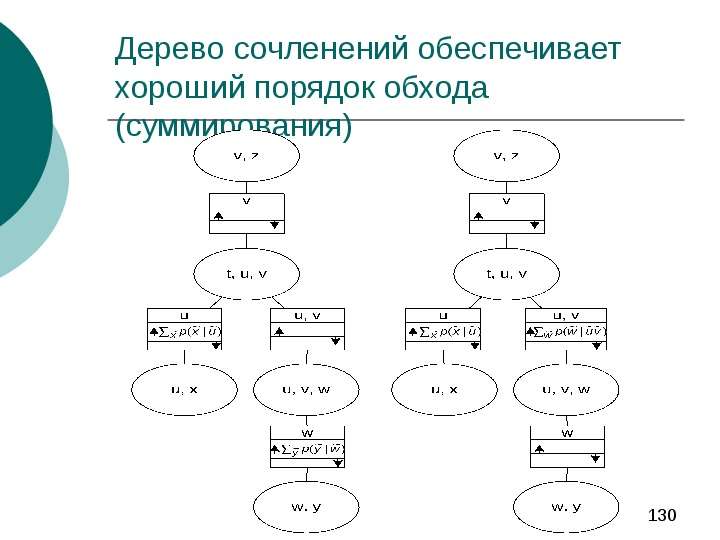
Содержание слайда: Первичная пропагация, обобщенный алгоритм «на пальцах»
Если мы хотим вычислить вероятность какого либо узла, то мы должны просуммировать совместное распределение по означиванию всех остальных переменных (маргинализовать).
Но, так как все наше распределение разбивается на произведение достаточно простых, можно проводить суммирование по очереди по одной (иногда по нескольким) переменным за раз, при этом большая часть сомножителей не будет от них зависеть.
№121 слайд


Содержание слайда: Первичная пропагация связь простого и обобщенного алгоритмов
Простой алгоритм — это всего лишь удачный порядок суммирования для обобщенного алгоритма.
Обобщенный алгоритм понадобится при появлении свидетельств.
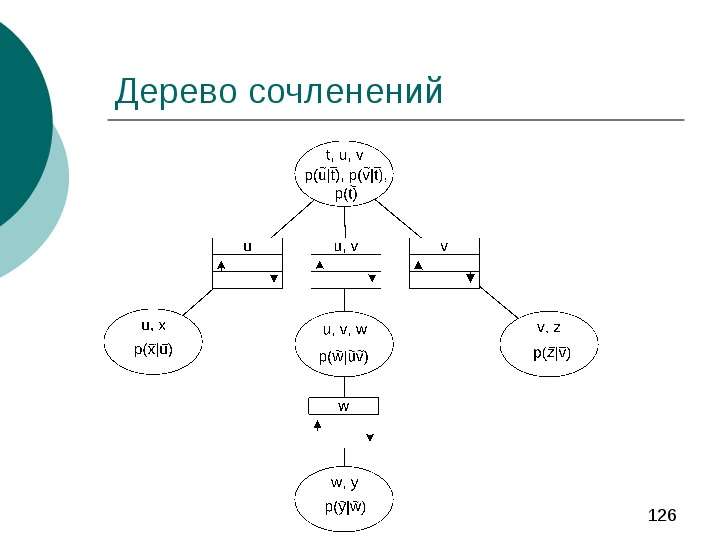
Для обобщенного алгоритма удобно определить на БСД структуру дерева смежности.
№128 слайд


Содержание слайда: Переход к пропагации свидетельств
Мы умеем вычислять маргинальные вероятности.
Давайте в процессе вычисления в нужном месте «заменим» «настоящую» вероятность единицей или нулем в зависимости от свидетельства.
Это гарантирует, что мы получим правильные вероятности в тех узлах, что ниже.
Как же учесть влияние на предшествующие узлы?
№133 слайд


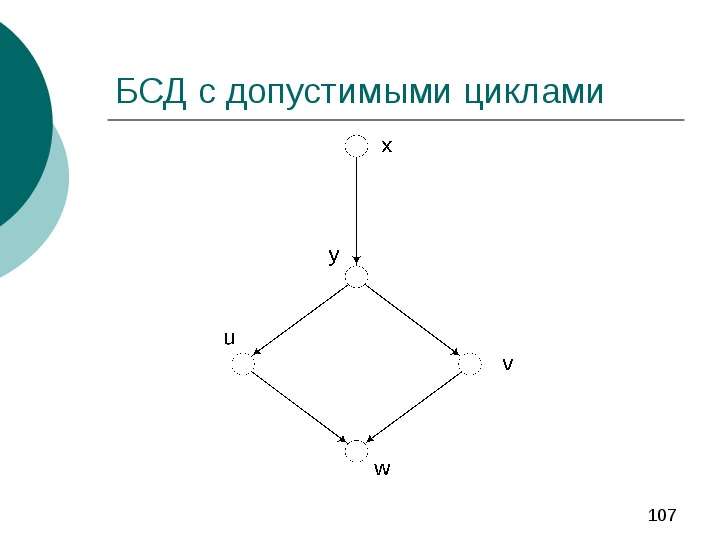
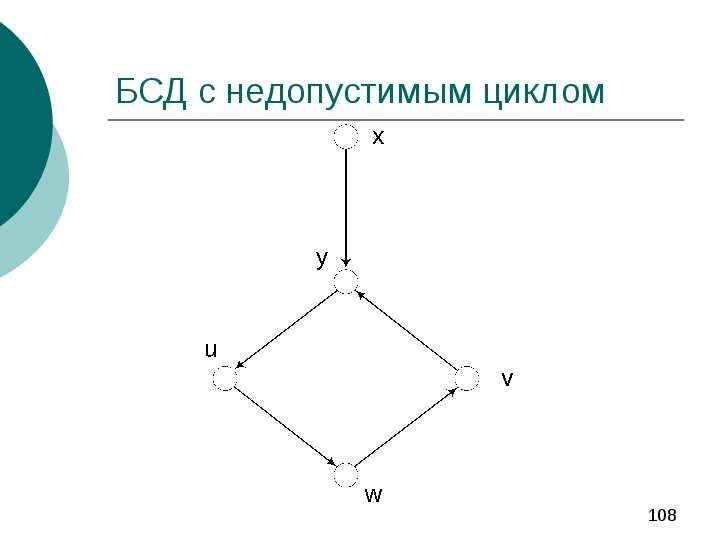
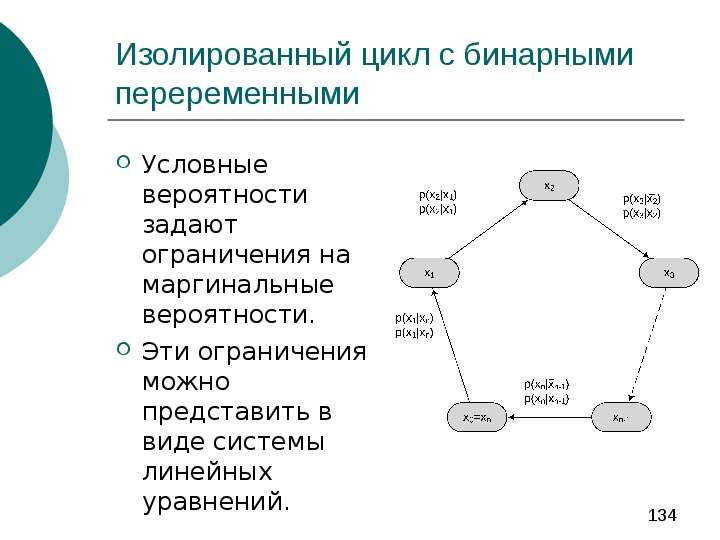
Содержание слайда: Проблема направленного цикла
Наличие направленного цикла в байесовской сети доверия приводит к тому, что chain rule не работает.
Но часто можно построить распределение, удовлетворяющее заданным условным вероятностям.
Такое распределение может быть не единственным: исходным данным может отвечать семейство распределений.
№151 слайд


Содержание слайда: Особенности материала
Части материала «масштабируются» под нужды конкретного курса и конкретной аудитории;
В возникающих экстремальных задачах используются объекты, знакомые математикам (а не насильно заимствованные из экономики);
Много задач для программирования, удобно для организации семинаров и практикумов;
«Неисчерпаемая тематика» для курсовых и дипломных работ
№161 слайд


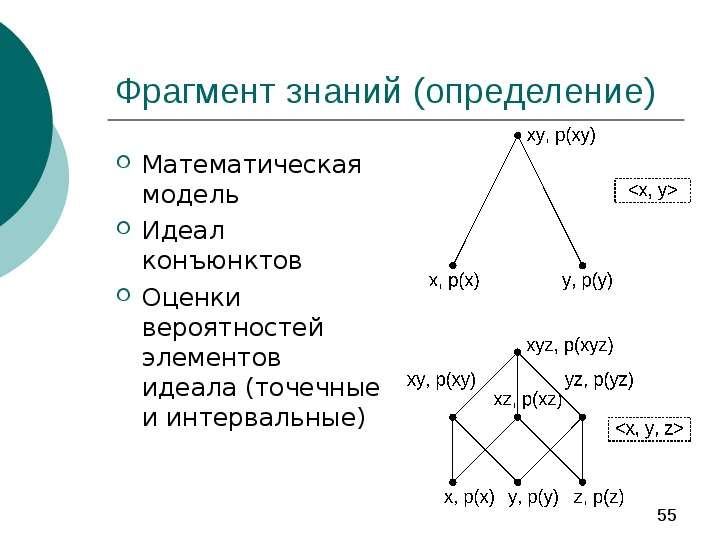
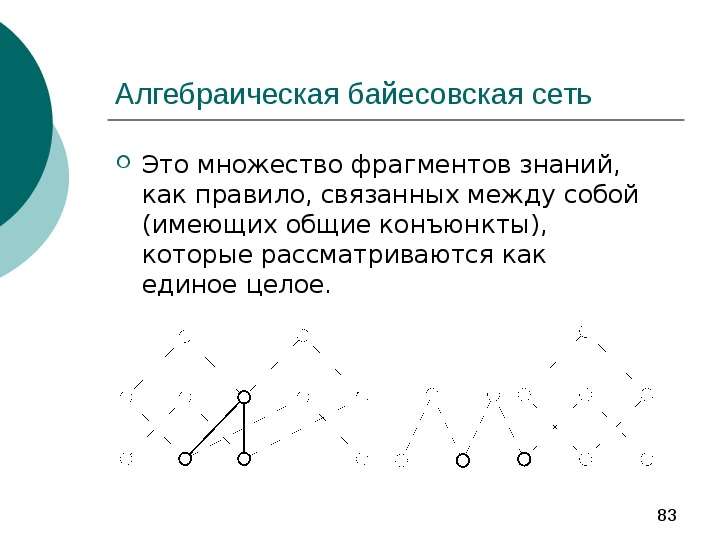
Содержание слайда: Декомпозируемость знаний
Эксперт не мыслит о закономерностях предметной области как о «связи всего со всеми»
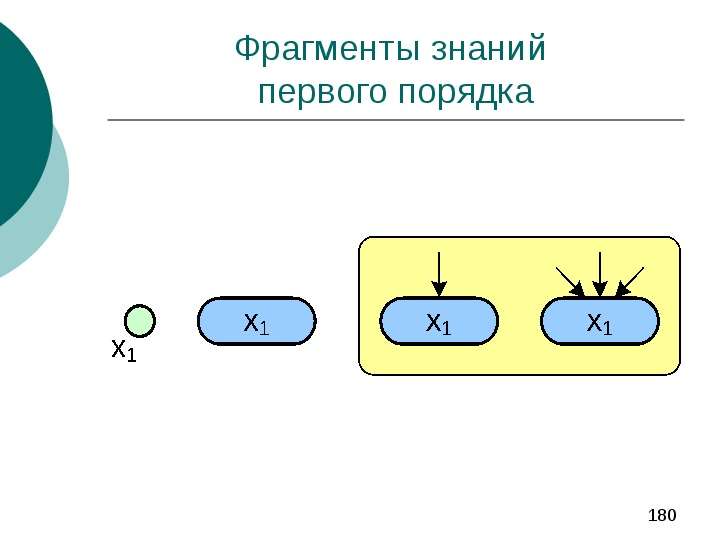
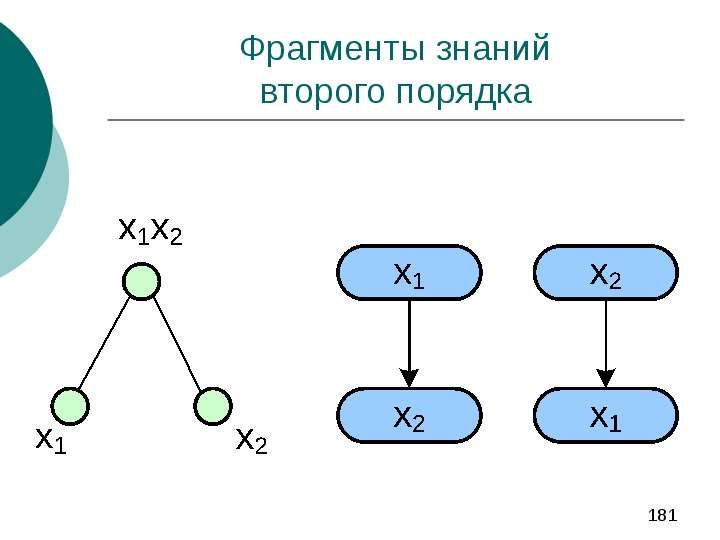
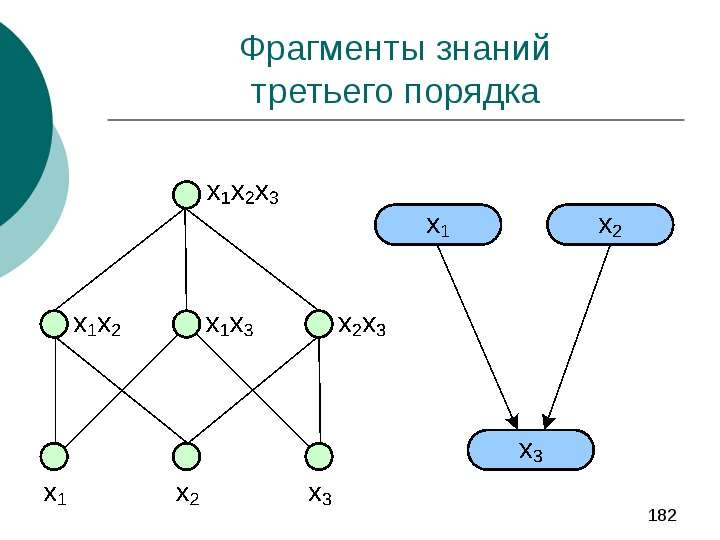
Выделяются фрагменты знаний (Knowledge patterns), которые содержат достаточно подробные сведения о небольшом числе объектов (или утверждений) о предметной области, а также о связях между ними
№162 слайд


Содержание слайда: Модель утверждения
Атомарная пропозициональная формула (булевская переменная, пропозициональная переменная, атомарная пропозиция) --- модель «атомарного» утверждения о предметной области
Пропозициональные формулы --- модели утверждений, возможно сложных, о предметной области
№164 слайд


Содержание слайда: Виды неопределенности
Существует много видов, например
неоднозначность и многозначность слов;
возможность двух или более интерпретаций записи даже на формальном языке;
недетерминированность;
нечёткость (в т.ч. лингвистическая);
неточность (интервальные оценки);
недоопределённость...
№166 слайд


Содержание слайда: Объект исследования
Высказывания, суждения, утверждения, представимые пропозициональными формулами над булевскими переменными;
Мера истинности которых характеризуется количественно с помощью вероятностных и/или небайесовских оценок;
Которые могут быть как точечные, так и интервальные [а в перспективе – твинные].
№167 слайд


Содержание слайда: Предмет исследования
Базы фрагментов знаний с неопределённостью;
Фрагмент знаний – некоторая [математическая] структура, состоящая из небольшого набора «тесно связанных» пропозициональных формул;
Мера истинности которых и теснота связи охарактеризована:
тензором условных вероятностей – БСД;
представлением тензора совместных вероятностей, допускающим точечные и интервальные оценки --- АБС;
[обобщение последнего на небайесовские меры истинности: нечёткую, доверия-правдоподобия, необходимости-возможности...]
№168 слайд


Содержание слайда: Логико-вероятностный подход (ЛВП)
Вероятностная мера как мера истинности
Точечные оценки значений вероятностной меры
Интервальные оценки значений вероятностной меры (как следствие неопределенности)
«Интервальная вероятность» и интервальная оценка вероятности
Единственность распределения и семейство распределений вероятности
№169 слайд


Содержание слайда: ЛВП --- богатая история
G. Boole, “An Investigation of the Laws of Thought, on Which Are Founded the Mathematical Theories of Logic and Probabilities” (1854)
N. Nilsson, Probabilistic Logic (AI, 1986)
N. Nilsson, Probabilistic Logic Revisited (AI, 1993)
De Finetti, Whaley, Ramsay, …
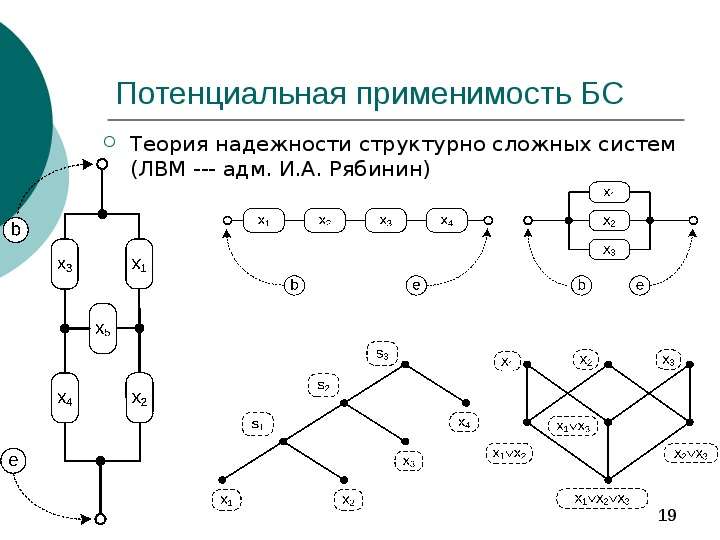
Школа логико-вероятностных методов в теории надежности (рук. адм. И. А. Рябинин) --- важнейшие приложения ЛВП.
Скачать все slide презентации ВВЕДЕНИЕ В БАЙЕСОВСКИЕ СЕТИ Алгоритмы для Интернета, ИТМО & СПбГУ С. -Петербург, 26 октября 2006 Рук. семинара Ю. М. Лифшиц одним архивом:
Похожие презентации
-
 Курс Введение в интернет-рекламу Лекция 2 Особенности продаж в сети интернет Алашкин Павел
Курс Введение в интернет-рекламу Лекция 2 Особенности продаж в сети интернет Алашкин Павел -
 Соцсети для e-commerce Уголок экспериментальной торговли
Соцсети для e-commerce Уголок экспериментальной торговли -
 Курс Введение в интернет-рекламу Лекция 3 Свойства рекламы в интернете Алашкин Павел
Курс Введение в интернет-рекламу Лекция 3 Свойства рекламы в интернете Алашкин Павел -
 Тексты для Интернета Аркадий Пильдес pildesgmail. com
Тексты для Интернета Аркадий Пильдес pildesgmail. com -
 Управление репутацией в поисковых системах Евгений Шевченко Интернет-агентство UaMaster Киев, 26 октября Банк Online acekievua uamaster. - презент
Управление репутацией в поисковых системах Евгений Шевченко Интернет-агентство UaMaster Киев, 26 октября Банк Online acekievua uamaster. - презент -
 Медиа-возможности в наружной рекламе Краткое руководство для операторов
Медиа-возможности в наружной рекламе Краткое руководство для операторов -
 Keeper Embedded – личный счет в любой социальной сети. Бизнес API для любого многопользовательского проекта.
Keeper Embedded – личный счет в любой социальной сети. Бизнес API для любого многопользовательского проекта. -
 Маяки для наблюдения за трещинами в несущих конструкциях зданий
Маяки для наблюдения за трещинами в несущих конструкциях зданий -
 FLRACE: УСКОРЕНИЕ 3D http://vk. com/flracegame Первая многопользовательская гоночная игра в формате 3D для социальных сетей
FLRACE: УСКОРЕНИЕ 3D http://vk. com/flracegame Первая многопользовательская гоночная игра в формате 3D для социальных сетей -
 Интернет в бизнесе или бизнес в Интернет?
Интернет в бизнесе или бизнес в Интернет?