Презентация Элементы математической статистики, комбинаторики и теории вероятностей. Простейшие вероятностные задачи онлайн

Содержание слайда: Глава 9. Элементы математической статистики, комбинаторики и теории вероятностей §51. Простейшие вероятностные задачи

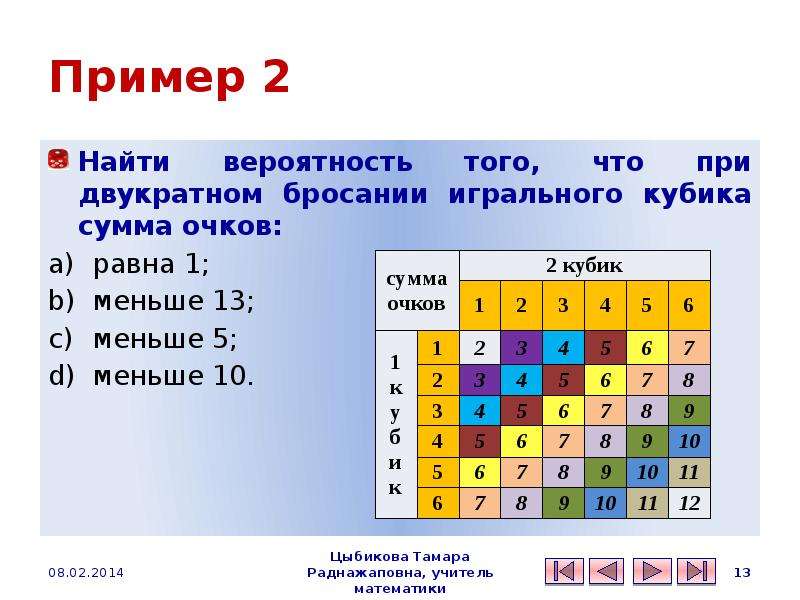
Содержание слайда: Содержание Классическое определение вероятности Алгоритм нахождения вероятности случайного события Обозначение вероятности: P(A) Пример 1. Найти вероятность того, что при одном бросании игрального кубика выпадет… Правило умножения Пример 2. Найти вероятность того, что при двукратном бросании игрального кубика сумма очков … Невозможное, достоверное и противоположное события Пример 3. Ученику предложили написать на доске любое двузначное число. Найти вероятность того, что это число …

Содержание слайда: Классическое определение вероятности Вероятностью события А при проведении некоторого испытания называют отношение числа тех исходов, в результате которого наступает событие А, к общему числу всех (равновозможных между собой) исходов этого испытания.

Содержание слайда: Алгоритм нахождения вероятности случайного события Для нахождения вероятности случайного события А при проведении некоторого испытания следует найти: число N всех возможных исходов данного испытания; количество N(A) тех исходов, в которых наступает событие A; Частное N(A)/N; оно и будет равно вероятности события А.

Содержание слайда: Обозначение вероятности: P(A) Probabilite (франц.)- вероятность, probably (англ.) – вероятно.

Содержание слайда: Пример 1 Найти вероятность того, что при одном бросании игрального кубика выпадет: 5 очков; четное число очков; число очков больше 4; число очков, не кратное 3.

Содержание слайда: Решение примера 1.a) Найти вероятность того, что при одном бросании игрального кубика выпадет: 5 очков; четное число очков; число очков больше 4; число очков, не кратное 3. РЕШЕНИЕ: Всего имеется N=6 (равновозможных) исходов: выпадение 1, 2, 3, 4, 5, 6. Ровно при одном из исходов произойдет интересующее нас событие A={выпадение 5 очков}. Значит, N(A)=1 и P(A)=N(A)/N=1/6. ОТВЕТ: 1/6

Содержание слайда: Решение примера 1.b) Найти вероятность того, что при одном бросании игрального кубика выпадет: 5 очков; четное число очков; число очков больше 4; число очков, не кратное 3. РЕШЕНИЕ: Всего имеется N=6 (равновозможных) исходов: выпадение 1, 2, 3, 4, 5, 6. Интересующее нас событие B={выпадение четного числа очков} произойдет в 3 случаях: когда выпадет 2, 4 или 6. Значит, N(B)=3 и P(A)=N(B)/N=3/6=1/2=0,5. ОТВЕТ: 0,5.

Содержание слайда: Решение примера 1.c) Найти вероятность того, что при одном бросании игрального кубика выпадет: 5 очков; четное число очков; число очков больше 4; число очков, не кратное 3. РЕШЕНИЕ: Всего имеется N=6 (равновозможных) исходов: выпадение 1, 2, 3, 4, 5, 6. Интересующее нас событие C={выпадение числа очков больше 4} произойдет в 2 случаях: когда выпадет 5 или 6. Значит, N(C)=2 и P(C)=N(B)/N=2/6=1/3. ОТВЕТ: 1/3.

Содержание слайда: Решение примера 1.d) Найти вероятность того, что при одном бросании игрального кубика выпадет: 5 очков; четное число очков; число очков больше 4; число очков, не кратное 3. РЕШЕНИЕ: Всего имеется N=6 (равновозможных) исходов: выпадение 1, 2, 3, 4, 5, 6. Из шести возможных выпавших чисел {1, 2, 3, 4, 5, 6} не кратны 3 только 4 числа: 1,2, 4, 5. Значит, N(D)=4 и P(D)=N(D)/N=4/6=2/3. ОТВЕТ: 2/3.

Содержание слайда: Правило умножения Для того чтобы найти число всех равновозможных исходов независимого проведения двух испытаний A и B, следует перемножить число всех исходов испытания A и число всех исходов испытания B.

Содержание слайда: Ключевые слова Невозможное событие Достоверное событие Противоположное событие

Содержание слайда: Пример 2 Найти вероятность того, что при двукратном бросании игрального кубика сумма очков: равна 1; меньше 13; меньше 5; меньше 10.

Содержание слайда:

Содержание слайда: Решение примера 2.a) Найти вероятность того, что при двукратном бросании игрального кубика сумма очков: равна 1; меньше 13; меньше 5; меньше 10. РЕШЕНИЕ: Минимальная возможная сумма равна 2, так что сумма никак не может быть равной 1. Значит, N(A)=0 и P(A)=0. ОТВЕТ: P(A)=0. Здесь мы имели дело с невозможным событием. Так называют событие, которое никогда не наступает при проведении данного испытания, его вероятность равна 0.

Содержание слайда: Решение примера 2.b) Найти вероятность того, что при двукратном бросании игрального кубика сумма очков: равна 1; меньше 13; меньше 5; меньше 10. РЕШЕНИЕ: Максимально возможное значение суммы равно 12. Значит, интересующее нас событие произойдет при любом исходе нашего опыта. Поэтому N(A)=N и P(A)=1. ОТВЕТ: P(A)=1 Здесь мы имеем дело с достоверным событием, т.е. событие обязательно наступит в данном испытании. Вероятность достоверного события равна 1.

Содержание слайда: Решение примера 2.c) Найти вероятность того, что при двукратном бросании игрального кубика сумма очков: равна 1; меньше 13; меньше 5; меньше 10. РЕШЕНИЕ: При каждом бросании кубика возможны 6 исходов. Предполагается, что результаты бросаний независимы друг от друга. По правилу умножения N=6*6=36 (равновозможных) исходов. Значит, интересующее нас событие произойдет при следующих 6 исходах: (1,1), (1,2), (1,3), (2,1), (2,2), (3,1). Поэтому N(A)=6 и P(A)=N(A)/N=6/36=1/6. ОТВЕТ: 1/6 Здесь мы имеем дело с независимым проведением двух испытаний.

Содержание слайда: Решение примера 2.d) Найти вероятность того, что при двукратном бросании игрального кубика сумма очков: равна 1; меньше 13; меньше 5; меньше 10. РЕШЕНИЕ: Вместо подсчета тех исходов, в которых наступает интересующее нас событие A, перечислим те исходы, в которых оно не наступает, т.е. сумма равна 10, 11 или 12: (4,6), (6,4), (5,5), (5,6), (6,5), (6,6). Поэтому N(A)=36-6=30 и P(A)=N(A)/N=30/36=5/6. ОТВЕТ: 5/6 Здесь мы имеем дело с противоположным событием. Так называют событие, которое наступает в том и только в том случае, когда не наступает интересующее нас событие.

Содержание слайда: События Событием называют невозможным, если оно никогда не наступает при проведении данного испытания. Вероятность невозможного события равна 0. Событием называют достоверным, если оно обязательно наступит в данном испытании. Вероятность достоверного события равна 1. Событием называют противоположным, если оно наступает в том и только в том случае, когда не наступает интересующее нас событие. Вероятность P(A) события A и вероятность P(Ᾱ) противоположного ему события Ᾱ связаны соотношением: P(A)+ P(Ᾱ) =1.

Содержание слайда: Пример 3 Ученику предложили написать на доске любое двузначное число. Найти вероятность того, что это число: не оканчивается нулем; состоит из различных цифр; не является квадратом целого числа; не делится на 17.

Содержание слайда:

Содержание слайда: Решение примера 3.a) Ученику предложили написать на доске любое двузначное число. Найти вероятность того, что это число: не оканчивается нулем; состоит из различных цифр; не является квадратом целого числа; не делится на 17. РЕШЕНИЕ: Всего имеется 90 двузначных чисел. N=90. Пусть А – интересующее нас событие, т.е. А={число не оканчивается нулем}, а Ᾱ - противоположное ему событие, т.е. Ᾱ= {число оканчивается нулем}= {10,20,…,90} . Следовательно, N(Ᾱ)=9 и P(Ᾱ)=N(Ᾱ)/N=9/90=0,9. Значит, P(А)=1-P(Ᾱ)=1-0,9=0,1. ОТВЕТ: 0,1

Содержание слайда: Решение примера 3.b) Ученику предложили написать на доске любое двузначное число. Найти вероятность того, что это число: не оканчивается нулем; состоит из различных цифр; не является квадратом целого числа; не делится на 17. РЕШЕНИЕ: Всего имеется 90 двузначных чисел. N=90. Пусть А – интересующее нас событие, т.е. А={число состоит из различных цифр}, а Ᾱ - противоположное ему событие, т.е. Ᾱ= {число состоит из одинаковых цифр}={11, 22, …, 99}. N(Ᾱ)=9. P(Ᾱ)=N(Ᾱ)/N=9/90=0,9. Значит, P(А)=1-P(Ᾱ)=1-0,9=0,1. ОТВЕТ: 0,1

Содержание слайда: Решение примера 3.c) Ученику предложили написать на доске любое двузначное число. Найти вероятность того, что это число: не оканчивается нулем; состоит из различных цифр; не является квадратом целого числа; не делится на 17. РЕШЕНИЕ: Всего имеется 90 двузначных чисел. N=90. Пусть А – интересующее нас событие, т.е. А={число не является квадратом целого числа}, а Ᾱ - противоположное ему событие, т.е. Ᾱ= {число является квадратом целого числа}= {16,25, 36, 49, 64, 81} . Следовательно, N(Ᾱ)=6 и P(Ᾱ)=N(Ᾱ)/N=6/90=1/15. Значит, P(А)=1-P(Ᾱ)=1-1/15=14/15. ОТВЕТ: 14/15.

Содержание слайда: Решение примера 3.d) Ученику предложили написать на доске любое двузначное число. Найти вероятность того, что это число: не оканчивается нулем; состоит из различных цифр; не является квадратом целого числа; не делится на 17. РЕШЕНИЕ: Всего имеется 90 двузначных чисел. N=90. Пусть А – интересующее нас событие, т.е. А={число не делится на 17}, а Ᾱ - противоположное ему событие, т.е. Ᾱ= {число делится на 17}= {17, 34, 51, 68, 85} . Следовательно, N(Ᾱ)=5 и P(Ᾱ)=N(Ᾱ)/N=5/90=1/18. Значит, P(А)=1-P(Ᾱ)=1-1/18=17/18. ОТВЕТ: 17/18.

Содержание слайда: Пример 4 Два ученика независимо друг от друга написали на доске по одному двузначному числу. Найдите вероятность того, что: эти два числа различны; сумма чисел равна 100; сумма чисел не больше 25; сумма чисел больше 190.

Содержание слайда: Решение примера 4.a) Два ученика независимо друг от друга написали на доске по одному двузначному числу. Найдите вероятность того, что: эти два числа различны; сумма чисел равна 100; сумма чисел не больше 25; сумма чисел больше 190. РЕШЕНИЕ: N=90*90=8100 (по правилу умножения) A={два числа различны}, Ᾱ={два числа одинаковы}={(10,10), (11,11),…, (99,99)}, 1 способ: N(Ᾱ)=90, следовательно, N(A)=N-N(Ᾱ)=90*90-90. Значит, P(A)=N(A)/N= (90*90-90)/(90*90)=(89*90)/(90*90)=89/90. 2 способ: N(Ᾱ)=90, P(Ᾱ)= N(Ᾱ)/N=90/(90*90)=1/90 . Значит, P(A)=1-P(Ᾱ)=1-1/90=89/90≈0,989. ОТВЕТ: 89/90

Содержание слайда: Решение примера 4.b) Два ученика независимо друг от друга написали на доске по одному двузначному числу. Найдите вероятность того, что: эти два числа различны; сумма чисел равна 100; сумма чисел не больше 25; сумма чисел больше 190. РЕШЕНИЕ: N=90*90=8100 (по правилу умножения) Если первый ученик выбрал число от 10 до 90, то интересующее нас событие произойдет, как только второй выберет недостающее до 100 слагаемое. Если первый ученик выбрал число, большее 90 (таких чисел 9), то при любом выборе второго сумма окажется больше 100, т.е. интересующее нас событие не произойдет. В остальных случаях, у второго ученика имеется по одной возможности составить сумму 100. Значит, N(A)=90-9=81, P(A)=81/8100=0,01. ОТВЕТ: 89/90

Содержание слайда: Решение примера 4.c) Два ученика независимо друг от друга написали на доске по одному двузначному числу. Найдите вероятность того, что: эти два числа различны; сумма чисел равна 100; сумма чисел не больше 25; сумма чисел больше 190. РЕШЕНИЕ: N=90*90=8100 (по правилу умножения). Перебор случаев (см. в таблице на следующем слайде): Если 1-й ученик выбрал 10, то 2-й ученик может выбрать число от 10 до 15 (6 случаев). Если 1-й ученик выбрал 11, то 2-й ученик может выбрать число от 10 до 14 (5 случаев). Для 12 будет 4 случая, для 13 – 3, для 14 – 2, для 15 – 1 случай. ВСЕГО: N(A)=6+5+4+3+2+1=21. P(A)=21/(90*90)=7/2700 ≈0,0026. ОТВЕТ: 7/2700

Содержание слайда:

Содержание слайда: Решение примера 4.d) Два ученика независимо друг от друга написали на доске по одному двузначному числу. Найдите вероятность того, что: эти два числа различны; сумма чисел равна 100; сумма чисел не больше 25; сумма чисел больше 190. РЕШЕНИЕ: N=90*90=8100 (по правилу умножения). Перебор случаев (см. в таблице на следующем слайде): Если 1-й ученик выбрал от 10 до 91, то при любом выборе 2-го ученика сумма не может больше 190, поскольку даже 91+99=190. Если 1-й ученик выбрал 92, то 2-й ученик может выбрать только одно число 99 (1 вариант). Если 1-й ученик выбрал 93, то 2-й ученик может выбрать только 2 числа: 98 или 99 (2 варианта). И т.д. Если 1-й ученик выбрал 99, то 2-й ученик может выбрать любое число от 92 до 99 (8 вариантов). ВСЕГО: N(A)=1+2+3+4+5+6+7+8=36. (см. таблицу на след.слайдах) P(A)=36/(90*90)=1/225 ≈0,0044. ОТВЕТ: 1/225

Содержание слайда:

Содержание слайда:

Содержание слайда: О комбинаторике Как мы видим, вычисление значений N и N(A) представляет определенные сложности. Прямое перечисление (выписывание, перебор) всех возможностей можно провести лишь в сравнительно небольшом количестве задач. Для подсчета количества различных комбинаций, удовлетворяющих тем или иным условиям, используются методы и факты комбинаторики. Довольно часто говорят, основы комбинаторики и теории вероятностей создали и разработали французские математики XVII века Пьер Ферма и Блез Паскаль.

Содержание слайда:

Содержание слайда: Рассмотрим задачу Ферма и Паскаль решали интересные задачи и в переписке между собой и с другими математиками обсуждали подходы к их решению, полученные результаты, связь с другими задачами, возможности применения в новых ситуациях и т.п. Рассмотрим задачу, которую можно отнести к задачам, с которых началось развитие теории вероятностей или, как еще тогда говорили, комбинаторного анализа. Её предложил Паскалю кавалер де Мере – весьма влиятельный деятель при дворе короля Людовика XIV.

Содержание слайда: Пример 5. Игральную кость бросают 4 раза. Что более вероятно: шестерка появится хотя бы 1 раз, или же, шестерка не появится ни разу?

Содержание слайда: Решение примера 5 По правилу умножения при четырехкратном бросании игральной кости N=6*6*6*6=64 =1296 исходов. Сама формулировка задачи ясно указывает на то, что мы имеем дело с парой противоположных друг другу событий. Что же обозначить за A, а что - Ᾱ? То событие, вероятность которого проще сосчитать, удобно обозначить А.

Содержание слайда: Решение примера 5 Что означает “появление шестерки хотя бы один раз“? Для появления шестерки много различных ситуаций: шестерка при третьем бросании, Шестерка при первом и третьем бросании и т.п. Не очень пока ясно, как их все пересчитать. Мы не будем этого делать.

Содержание слайда: Решение примера 5 Пусть событие А= {шестерка не появится ни разу}. Это означает, что при каждом из 4 бросков имеется ровно 5 исходов: выпадение 1, 2, 3, 4, 5. По правилу умножения: N(A)=5*5*5*5=54=625. Значит, P(A)=54/64=625/1296≈0,4823; P(Ᾱ)=1-P(A)=1-0,4823≈0,5177. Таким образом, P(Ᾱ)>P(A). ОТВЕТ: появление хотя бы одной шестерки более вероятно, чем полное отсутствие шестерок при четырех бросаниях игральной кости.

Содержание слайда: Можно и так решить задачу:

Содержание слайда: Для 3 бросаний ответ другой P(A)=53/63=125/216; P(Ᾱ)=1-P(A)=1-125/216=91/216. Таким образом, P(Ᾱ)<P(A). ОТВЕТ: полное отсутствие шестерок более вероятно, чем появление хотя бы одной шестерки при трех бросаниях игральной кости.

Содержание слайда: Пьер Ферма (1601-1665)

Содержание слайда: Блез Паскаль (1623-1662)

Содержание слайда:

Содержание слайда: Для учителей математики Название §51 «Простейшие вероятностные задачи» в учебнике для 10—11 классов совпадает с названием §20 в учебнике для 9 класса. Эти параграфы совпадают между собой и по содержанию: вероятность как модель реальных случайных событий, классическое определение вероятности, алгоритм вычисления вероятности по этому определению, связь между вероятностью события и противоположного ему события — вот основные акценты в §51. В то же время прямых цитирований из учебника для 9 класса нет. Тем самым уже известный из основной школы учебный материал повторяется и закрепляется на новом массиве примеров и задач.

Содержание слайда: Для учителей математики Термин «простейшие» в применении к вероятностным задачам означает отсутствие формульной комбинаторики (числа размещений и сочетаний). Во всех примерах и задачах этого параграфа вполне хватает правила умножения, формулировка которого мы, разумеется, повторяется и в данном учебнике для старшей школы. Поэтому, несмотря на присутствие термина «вероятностные» в названии параграфа, с учебной точки зрения в §51 закрепляется умение работать с простейшими комбинаторными ситуациями: проводить непосредственный перебор всех случаев, разумно организовывать перебор и использовать правило умножения. Пожалуй, единственным отличием является отсутствие дерева всевозможных вариантов. Этот материал остается в основной школе.

Содержание слайда: Для учителей математики Рассмотрение цепочки последовательно усложняющихся комбинаторных примеров подводит к необходимости расширить имеющийся технический аппарат комбинаторики. Грубо говоря, становится уже тесновато действовать в рамках лишь перебора и правила умножения. Тем самым структурно §51 образует мостик между материалом в той или иной мере известным из курса основной школы и новыми для учеников понятиями размещения и сочетания. Хотелось бы обратить специальное внимание на пример 5: «Игральную кость бросают четыре раза. Что более вероятно: то, что шестерка появится хотя бы один раз, или же, что шестерка не появится ни разу?» Он интересен с исторической точки зрения, так как послужил одной из отправных точек к созданию в XVII веке теории вероятностей.

Содержание слайда: Для учителей математики Важен он и содержательно, так как по существу является одной из простейших схем Бернулли независимого повторения испытания с двумя исходами, т. е. является своего рода пропедевтикой материала §54, заключительного в этой главе. Кроме того, в анализе этого примера ясно указано, что основой решения является (в очередной раз!) правило умножения. Если действовать предполагая, что теорема Бернулли заранее известна, то ответ для вероятности того, что шестерка не появится ни разу, следовало бы получить как Р(А)=(5/6)4 . Мы получаем тот же ответ, но как Р(А)=54/64, где для вычисления и числителя, и знаменателя применяется уже хорошо известное правило умножения.

Содержание слайда: Для учителей математики В §52, формально, приведены сведения об использовании двух, пожалуй наиболее знакомых большинству учителей, комбинаторных формул (см.вверху). Во многих УМК для школы при изложении этого учебного материала авторы выбирают стиль, близкий к справочной литературе. А именно, кратко формулируют определения того, что именно обозначается символами С* и А*, сообщают две приведенные выше формулы и дают несколько примеров их использования. Нет сомнений, что это самый короткий путь к использованию указанных формул при решении задач. Зачастую такой комбинаторный «ликбез» проводится и в 9 классе, а в некоторых УМК даже и в 7 классе.

Содержание слайда:

Содержание слайда:

Содержание слайда: Источники Алгебра и начала анализа, 10-11 классы, Часть 1. Учебник, 10-е изд. (Базовый уровень), А.Г.Мордкович, М., 2009 Алгебра и начала анализа, 10-11 классы. (Базовый уровень) Методическое пособие для учителя, А.Г.Мордкович, П.В.Семенов, М., 2010 Таблицы составлены в MS Word и MS Excel. Интернет-ресурсы ЕГЭ 2013. Математика. Задача В10. Теория вероятностей. Рабочая тетрадь. Изд. второе, дополненное. Под ред. А.Л.Семенова и И.В. Ященко, М., Изд. МЦНМО, 2013