Презентация Неопределенный интеграл, его свойства и вычисление. Первообразная и неопределенный интеграл онлайн

На нашем сайте вы можете скачать и просмотреть онлайн доклад-презентацию на тему Неопределенный интеграл, его свойства и вычисление. Первообразная и неопределенный интеграл абсолютно бесплатно. Урок-презентация на эту тему содержит всего 89 слайдов. Все материалы созданы в программе PowerPoint и имеют формат ppt или же pptx. Материалы и темы для презентаций взяты из открытых источников и загружены их авторами, за качество и достоверность информации в них администрация сайта не отвечает, все права принадлежат их создателям. Если вы нашли то, что искали, отблагодарите авторов - поделитесь ссылкой в социальных сетях, а наш сайт добавьте в закладки.

Презентации » Математика » Неопределенный интеграл, его свойства и вычисление. Первообразная и неопределенный интеграл

Просмотр ВСЕЙ презентации! ЖМИТЕ

Оцените презентацию от 1 до 5 баллов!

Смотреть онлайн
Скачать

Тип файла:

ppt / pptx (powerpoint)
Всего слайдов:

89 слайдов
Для класса:

1,2,3,4,5,6,7,8,9,10,11
Размер файла:

1.03 MB
Просмотров:

146
Скачиваний:

4
Автор:

неизвестен

Слайды и текст к этой презентации:

№1 слайд

Содержание слайда: Прикладная математика каф. МЕН Аношина О.В.

№2 слайд

Содержание слайда: Основная литература 1. Шипачев В. С. Высшая математика. Базовый курс: учебник и практикум для бакалавров [Гриф Минобразования РФ] / В. С. Шипачев; под ред. А. Н. Тихонова. - 8-е изд., перераб. и доп. - Москва : Юрайт, 2015. - 447 с. 2. Шипачев В. С. Высшая математика. Полный курс: учебник для акад. бакалавриата [Гриф УМО] / В. С. Шипачев; под ред. А. Н. Тихонова. - 4-е изд., испр. и доп. - Москва : Юрайт, 2015. - 608 с 3. Данко П.Е., Попов А.Г., Кожевникова Т..Я. Высшая математика в упражнениях и задачах. [Текст] / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. В 2 ч. – М.: Высшая школа, 2007. – 304+415c.

№3 слайд

Содержание слайда: Отчетность Контрольная работа. Выполняется в соответствии: Задания и методические указания к выполнению контрольных работ по дисциплине «Прикладная математика», Екатеринбург, ФГАОУ ВО «Российский государственный профессионально-педагогический университет», 2016 - 30с. Вариант контрольной работы выбирать по последней цифре номера зачетной книжки. 2. Экзамен

№4 слайд

Содержание слайда: Неопределенный интеграл, его свойства и вычисление Первообразная и неопределенный интеграл

№5 слайд

Содержание слайда:

№6 слайд

Содержание слайда:

№7 слайд

Содержание слайда:

№8 слайд

Содержание слайда: Свойства интеграла Производная неопределенного интеграла равна подынтегральной функции, а его дифференциал- подынтегральному выражению. Действительно:

№9 слайд

Содержание слайда: Свойства интеграла 3. Неопределенный интеграл от дифференциала непрерывно дифференцируемой функции равен самой этой функции с точностью до постоянной: так как является первообразной для

№10 слайд

Содержание слайда: Свойства интеграла

№11 слайд

Содержание слайда: Таблица неопределенных интегралов

№12 слайд

Содержание слайда: Таблица неопределенных интегралов

№13 слайд

Содержание слайда: Свойства дифференциалов При интегрировании удобно пользоваться свойствами:

№14 слайд

Содержание слайда: Примеры

№15 слайд

Содержание слайда: Примеры

№16 слайд

Содержание слайда: Независимость от вида переменной

№17 слайд

Содержание слайда: Пример Вычислим

№18 слайд

Содержание слайда: Методы интегрирования Интегрирование по частям

№19 слайд

Содержание слайда: Примеры

№20 слайд

Содержание слайда: Примеры

№21 слайд

Содержание слайда: Метод замены переменной

№22 слайд

Содержание слайда: Интегрирование функций, содержащих квадратный трехчлен

№23 слайд

Содержание слайда: Пример

№24 слайд

Содержание слайда: Пример Найти

№25 слайд

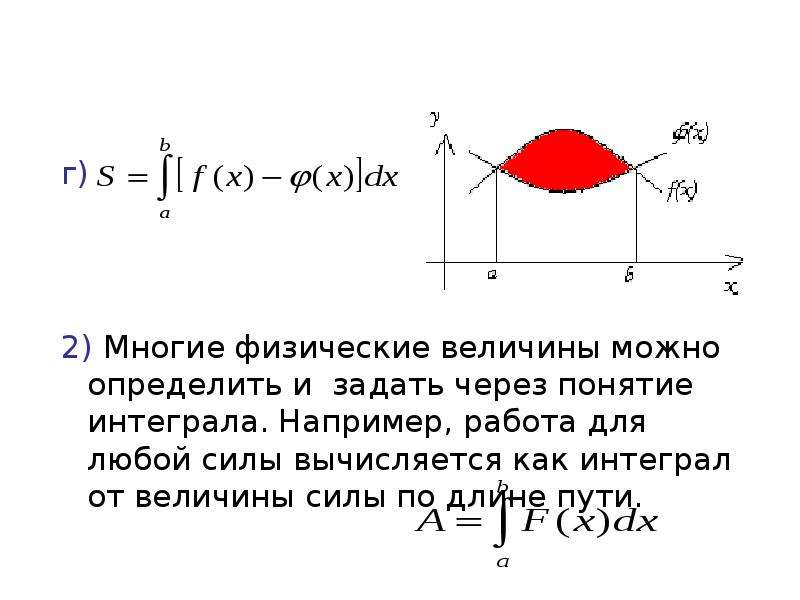
Содержание слайда: Определенный интеграл, его основные свойства. Формула Ньютона- Лейбница. Приложения определенного интеграла. К понятию определенного интеграла приводит задача нахождения площади криволинейной трапеции. Пусть на некотором интервале [a,b] задана непрерывная функция Задача: Построить ее график и найти F площадь фигуры, ограниченной этой кривой, двумя прямыми x = a и x = b, а снизу – отрезком оси абсцисс между точками x = a и x = b.

№26 слайд

Содержание слайда:

№27 слайд

Содержание слайда: Определение Под определенным интегралом от данной непрерывной функции f(x) на данном отрезке [a;b] понимается соответствующее приращение ее первообразной, то есть Числа a и b – пределы интегрирования, [a;b] – промежуток интегрирования.

№28 слайд

Содержание слайда: Правило: Определенный интеграл равен разности значений первообразной подынтегральной функции для верхнего и нижнего пределов интегрирования. Введя обозначения для разности

№29 слайд

Содержание слайда: Основные свойства определенного интеграла. 1)Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. где x и t – любые буквы. 2)Определенный интеграл с одинаковыми пределами интегрирования равен нулю

№30 слайд

Содержание слайда: 3) При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный 3) При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный (свойство аддитивности) 4) Если промежуток [a;b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутку [a;b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.

№31 слайд

Содержание слайда: 5)Постоянный множитель можно выносить за знак определенного интеграла. 5)Постоянный множитель можно выносить за знак определенного интеграла. 6)Определенный интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.

№32 слайд

Содержание слайда: 3. Замена переменной в определенном интеграле. где для , функции и непрерывны на Пример: = =

№33 слайд

Содержание слайда: Несобственные интегралы. Определение. Пусть функция f(x) определена на бесконечном интервале [a; + ) и интегрируется на любом интервале [a;b], где b < + . Если существует , то этот предел называется несобственным интегралом функции f(x) на интервале [a; + ) и обозначается .

№34 слайд

Содержание слайда: Таким образом, по определению, Таким образом, по определению, Если этот предел - некоторое число, то интеграл называется сходящимся, если предела не существует, или он равен , то говорят, что интеграл расходится.

№35 слайд

Содержание слайда: Пример. Интеграл Пуассона: если а = 1, то Интеграл сходится, и его значение .

№36 слайд

Содержание слайда: 5. Приложения определенного интеграла 1) Площадь плоских фигур. а) если б) если в)

№37 слайд

Содержание слайда: г) г) 2) Многие физические величины можно определить и задать через понятие интеграла. Например, работа для любой силы вычисляется как интеграл от величины силы по длине пути.

№38 слайд

Содержание слайда: ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ Если каждой паре (x,y) значений двух независимых переменных из области D ставится определенное значение z, то говорят, что z есть функция двух переменных (x,y).

№39 слайд

Содержание слайда: Частные приращения и частные производные

№40 слайд

Содержание слайда: Полное приращение функции 2-х переменных Если обеим переменным дать приращение, то функция получит полное приращение

№41 слайд

Содержание слайда: Полное приращение и полный дифференциал

№42 слайд

Содержание слайда: Дифференциалы высшего порядка Дифференциалом второго порядка функции z=f(x,y) называется Вообще: Если х и у независимые переменные, то .

№43 слайд

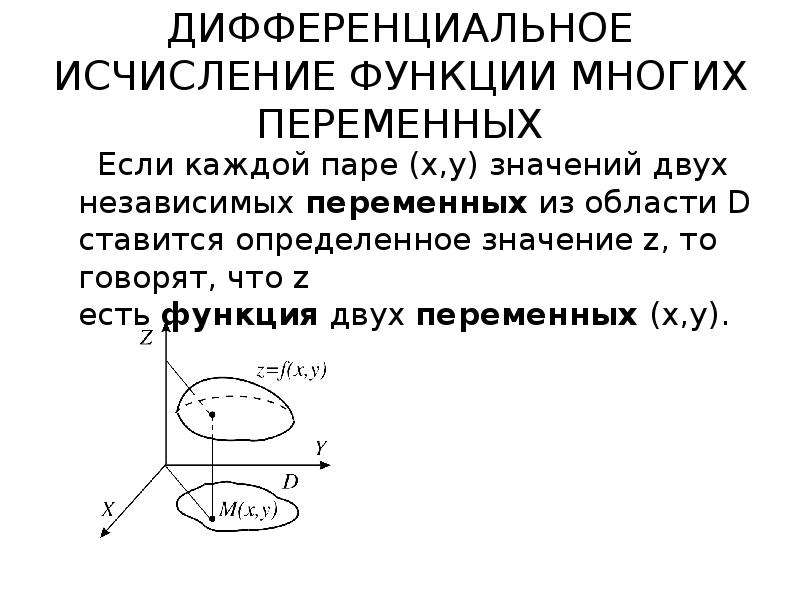
Содержание слайда: Экстремумы функции двух переменных Определение. Говорят, что в точке функция f (x,y) имеет максимум, если cуществует такая окрестность этой точки, что для всех точек P(x,y) этой окрестности, отличных от , выполнено неравенство Аналогично определяется минимум функции. Минимум и максимум функции называются ее экстремумами.

№44 слайд

Содержание слайда: Экстремумы функции двух переменных Теорема (необходимое условие экстремума). В точке экстремума функции нескольких переменных каждая ее частная производная либо равна нулю, либо не существует. Точки, в которых выполнены эти условия, называются критическими.

№45 слайд

Содержание слайда: Достаточные условия экстремума функции двух переменных Теорема. Пусть функция z=f(x,y) определена и имеет непрерывные частные производные до 3-го порядка в некоторой окрестности точки , в которой . Если при этом в этой точке выполнено условие , то точка является точкой экстремума функции, причем точкой максимума, если , и точкой минимума, если . Если же в этой точке , то экстремума в точке нет. В том случае, если в точке , теорема ответа не дает.

№46 слайд

Содержание слайда: Пример Исследовать на экстремум функцию

№47 слайд

Содержание слайда: Наибольшее и наименьшее значения функции Определение. Наименьшее или наибольшее значение функции в данной области называется абсолютным экстремумом функции (абсолютным минимумом или абсолютным максимумом соответственно) в этой области.

№48 слайд

Содержание слайда: Известно, что непрерывная в замкнутой ограниченной области функция достигает в ней своих наибольшего и наименьшего значений. Известно, что непрерывная в замкнутой ограниченной области функция достигает в ней своих наибольшего и наименьшего значений. Абсолютный экстремум достигается функцией либо в критических точках, либо на границе области.

№49 слайд

Содержание слайда: Пусть функция непрерывна в замкнутой ограниченной области G, дифференцируема внутри этой области. Чтобы найти наибольшее и наименьшее значения функции в этой области, нужно: Пусть функция непрерывна в замкнутой ограниченной области G, дифференцируема внутри этой области. Чтобы найти наибольшее и наименьшее значения функции в этой области, нужно: 1)найти критические точки, принадлежащие этой области, и вычислить в них значения функции; 2)найти наибольшее и наименьшее значения функции на границе области; 3)из всех найденных значений выбрать наибольшее и наименьшее.

№50 слайд

Содержание слайда: Скалярное поле Основные определения Пусть в области D пространства Охуz задана функция u=u(х,у,z). В этом случае говорят, что в области D задано скалярное поле, а саму функцию u=u(х,у,z)называют функцией поля. Например, поле давлений, температур и т.д.

№51 слайд

Содержание слайда: Скалярное поле Основные определения Множество точек М области D, для которых скалярное поле сохраняет постоянное значение, т. е. u(М)=С, называется поверхностью уровня ( или изоповерхностью) скалярного поля.

№52 слайд

Содержание слайда: Если область D расположена на плоскости Оху, то поле u=u(х,у) является плоским. Если область D расположена на плоскости Оху, то поле u=u(х,у) является плоским. Поверхности уровня называют в этом случае линиями уровня.

№53 слайд

Содержание слайда: Пусть Пусть

№54 слайд

Содержание слайда: Линии уровня Пусть . Линии уровня этой поверхности имеют вид

№55 слайд

Содержание слайда: Пусть дан конус Пусть дан конус

№56 слайд

Содержание слайда: Линии уровня конуса

№57 слайд

Содержание слайда: Пусть задана дифференцируемая функция скалярного поля. Пусть задана дифференцируемая функция скалярного поля. Рассмотрим точку этого поля и луч , выходящий из точки P в направлении единичного вектора где –углы, образованные вектором с осями координат .

№58 слайд

Содержание слайда: Определение

№59 слайд

Содержание слайда: Производной функции Производной функции в точке P по направлению называется предел отношения приращения функции в направлении к величине перемещения при : .

№60 слайд

Содержание слайда: Вычисление производной по направлению Формула вычисления производной по направлению:

№61 слайд

Содержание слайда: Градиент скалярного поля Градиентом скалярного поля u=u(x,y,z), где u=u(x,y,z)-дифференцируемая функция, называется вектор с координатами . Таким образом, или .

№62 слайд

Содержание слайда: Пример Найти градиент функции u= в точке M(6,2,3). Решение. Вычислим градиент функции. Тогда grad u = + + А в точке М

№63 слайд

Содержание слайда: Направление градиента Теорема. Производная функции по направлению равна проекции градиента этой функции на данное направление (в соответствующей точке).

№64 слайд

Содержание слайда: Направление градиента Так как производная по направлению представляет собой скорость изменения функции в данном направлении , а проекция вектора на другой вектор имеет максимальное значение, если оба вектора совпадают по направлению, то градиент функции в данной точке указывает направление наиболее быстрого возрастания функции.

№65 слайд

Содержание слайда: Величина градиента плоского скалярного поля Величина градиента плоского скалярного поля ,т.е.  grad u  = обозначается tg и определяет крутизну наибольшего ската или подъема поверхности u = f (x, y).

№66 слайд

Содержание слайда: Градиент скалярного поля в данной точке по величине и направлению равен максимальной скорости изменения поля в этой точке, т. е. , где .

№67 слайд

Содержание слайда: Обыкновенные дифференциальные уравнения Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x, неизвестной функции y = f(x) и её производных (или дифференциалов):

№68 слайд